
|
 |
|
Система домов Плацидуса Не корректный метод расчета примарных дирекций Правильный метод Плацидуса Зодиакальные дирекции в системе Плацидуса Дирекции с учетом широты в системе Плацидуса Мунданные параллели в системе Плацидуса Мунданные дирекции с произвольным аспектом |
||||||||||||||||||||||
| В системе Плацидуса 11-й и 3-й куспиды домов являются точками
эклиптики в Четвертом и Первом квадрантах (соответственно), чьё отношение меридианного
расстояния к полудуге равно 1/3. Также 12-й и 2-й куспиды домов являются точками эклиптики в
Четвертом и Первом квадранте (соответственно), чьё отношение MD к SA равно 2/3. Здесь "MD/SA"
означает UMD/DSA для точки находящейся выше горизонта и LMD/NSA для точки находящейся ниже
горизонта, то есть в этом контексте MD может превышать 90. Таким образом куспиды домов
Плацидуса являются точками эклиптики, которые продвинулись на 1/3 и 2/3 своего пути через
соответствующий им квадрант. |
||||||||||||||||||||||
| Не корректный метод расчета примарных дирекций 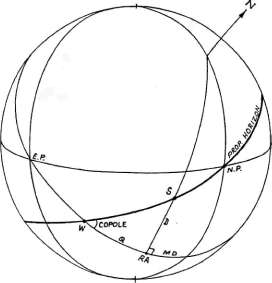 Рисунок 7-1 Пропорциональным горизонтом называется местоположение
точек на небесной сфере, которые имеют одинаковое отношение меридианного расстояния к полудуге
тела (рисунок 7-1). Пусть W будет точкой пересечения (и её RA) пропорционального горизонта тела
с экватором. Пусть Q будет разницей между W тела и его RA. Меридианное расстояние
W будет равно: MD(w)= Q + MD, где МD является меридианным расстоянием тела. Так как W является
точкой на экваторе, её склонение равно нулю и её полудуга равна 90. А так как отношение MD(w) к SA(w)
должно равняться отношению MD к SA тела (так как по определению W лежит на пропорциональном
горизонте тела S), имеем: 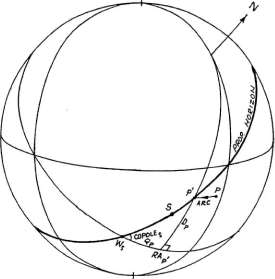 Рисунок 7-2 Пусть RA(p') будет равняться RA точки
пересечения дневного круга промиссора с пропорциональным горизонтом сигнификатора.
Пусть Q(p) будет разницей между RA(p') и W(s). Рассмотрим треугольник,
сторонами которого являются дуги экватора (=Q(p)), часового круга через
Р' (=D(p)) и пропорционального горизонта сигнификатора. Угол между экватором
и пропорциональным горизонтом равняется со-полюс(s). Далее: 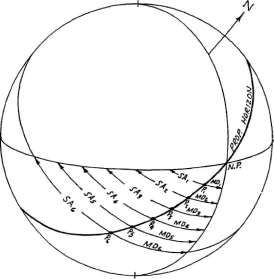 Рисунок 7-3 Сейчас рассмотрим рисунок 7-3, которая показывает полудуги и меридианные расстояния нескольких точек, которые находятся на разных дневных кругах (имеют разное склонение), но которые все лежат на одном и том же пропорциональном горизонте (то есть они имеют одинаковое отношение MD к SA). Заметьте, что точки расположены вдоль пропорционального горизонта по направлению к меридиану (от Р6 до Р1), MD уменьшается и следовательно SA должно уменьшаться также, для поддержания постоянной пропорции; поэтому любой пропорциональный горизонт должен проходить через точки Севера (и Юга) на горизонте, или по крайней мере приближаться к этим точкам, как к пределу. Поэтому пропорциональный горизонт в не корректном методе Плацидуса должен быть домовым кругом и поэтому Q и W тела в не корректном методе Плацидуса должны быть такими же как Q и W тела в системе Кампануса-Регимонтануса. Однако из выше описанных примеров становится видно, что они не равны:
Такое расхождение получается потому что пропорциональный
горизонт в не корректном методе Плацидуса считается большим кругом (проходящим через центр Земли).
А раз большой круг, значит может быть домовым кругом. На самом деле пропорциональный горизонт не
является большим кругом и поэтому не корректно использовать правила тригонометрии для больших кругов
(правила Нейпира) для решения треугольника при нахождении полюс(s) и Q(p). Система Плацидуса является
единственной не проекционной системой, рассмотренной в этой книге, то есть единственной системой,
в которой местоположение точек с равной Мунданной позицией не является большим кругом на небесной
сфере. |
||||||||||||||||||||||
| Для нахождения дирекции промиссора
Р к мунданному соединению с сигнификатором S необходимо определить точку
Р' на дневном круге промиссора, которая имеет такое же отношение MD к
SA, как и сигнификатор, то есть MD(p')/SA(p') = MD(s)/SA(s). Тогда дуга
дирекции будет равна RA(p) - RA(p'). Учтите, что Р и S находятся в Первом
квадранте, так что ночные полудуги используются. Следовательно SA(p')=90-AD(p)
потому что D(p') = D(p), где AD(p) является разницей восхождений промиссора.
Также MD(p')=RAIC-RA(p'), следовательно RAIC-RA(p')=(90-AD(p))*MD(s)/SA(s),
откуда:
Заметьте, что если МС является сигнификатором, тогда MD(s) =0,
следовательно ARC= RA(p) - RAMC. Также если Асцендент является сигнификатором, тогда MD(s)/SA(s) =1,
следовательно |
||||||||||||||||||||||
| Зодиакальные дирекции в системе Плацидуса Для нахождения долготы точки аспекта в зодиакальной
дирекции величина аспекта прибавляется к долготе промиссора. Используя полученную долготу
точки аспекта по формуле А2 и А4 определяем RA и склонение точки аспекта. Используя склонение точки
аспекта, по формуле 1-1 определяем AD точки аспекта, далее продолжаем вычисления как для
мунданного соединения, используя RA и AD точки аспекта для RA(p) и AD(p). |
||||||||||||||||||||||
| Дирекции с учетом широты в системе Плацидуса Для нахождения долготы точки аспекта в дирекции с учетом
широты величина аспекта прибавляется к долготе промиссора. Полученная долгота используется
совместно с широтой тела на момент аспекта в формуле А5 и А6 для нахождения склонения и RA точки
аспекта. Используя склонение точки аспекта по формуле 1-1 вычисляется AD точки аспекта, далее
продолжаем вычисления как для мунданного соединения, используя RA и AD
точки аспекта для RA(p) и AD(p). |
||||||||||||||||||||||
| Мунданные параллели в системе Плацидуса В системе Плацидуса две точки считаются находящимися в
Мунданной параллели если они лежат с противоположных сторон меридиана, но находятся с одной и
той же стороны горизонта и имеют одинаковое отношение MD/SA. Мунданная контрпараллель имеет
место когда две точки находятся с одной и той же стороны меридиана, но по разные стороны горизонта
и имеют одинаковое отношение MD/SA. |
||||||||||||||||||||||
| Мунданные дирекции с произвольным аспектом в системе Плацидуса Для вычисления мунданной дирекции с произвольным аспектом в системе Плацидуса удобно ввести понятие Мунданной позиции Плацидуса (РМР) сигнификатора следующим образом:
Найдем дирекцию промиссора Р к мунданному аспекту с сигнификатором S. Пусть Мунданная позиция Плацидуса точки аспекта будет равна: РМР(ар)=РМР(s)+А, где РМР(s) является Мунданной позицией Плацидуса сигнификатора, а А является величиной аспекта. Далее, найдем MD/AS отношение для вычисленного значения РМР(ар):
Далее процесс вычисления продолжается
как для Мунданного соединения, используя полученное MD/SA отношение точки
аспекта в качестве МD/SA сигнификатора, и используя значения T, V и R
в зависимости от квадранта, в котором точка аспекта лежит, а имеено: 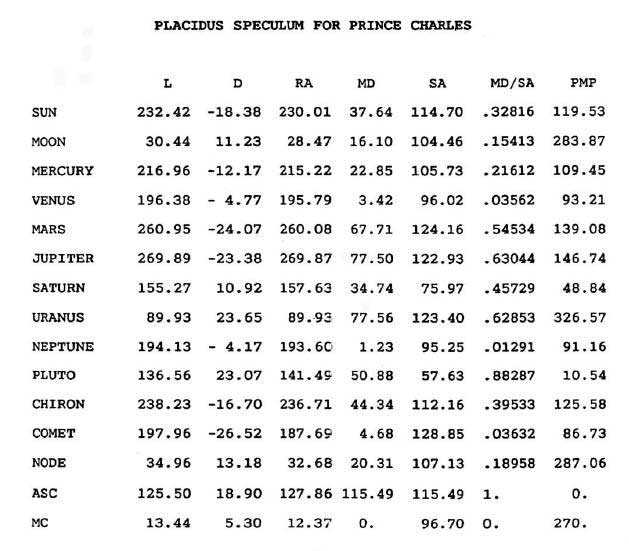
|
||||||||||||||||||||||
| Наверх Оглавление |
||||||||||||||||||||||
|
Copyright© 2004 STELLIUM.RU Webmaster |
||||||||||||||||||||||