
|
 |
|
Меридианная система Мунданное соединение в Меридианной системе Мунданные дирекции с произвольным аспектом в Меридианной системе Зодиакальные дирекции и дирекции с учетом широты в Меридианной системе Мунданные параллели в Меридианной системе Система домов Моринуса Мунданное соединение в системе Морисона Зодиакальные дирекции и дирекции с учетом широты в системе Моринуса Мунданные дирекции с произвольным аспектом в системе Моринуса Мунданные параллели в системе Моринуса Равнодомная система домов Система домов Порфирия Cистема домов Алкабитуса Система домов Коха Мунданное соединение в системе Коха Зодиакальные дирекции в системе Коха Дирекции с учетом широты в системе Коха Мунданные дирекции с произвольным аспектом в системе Коха |
||
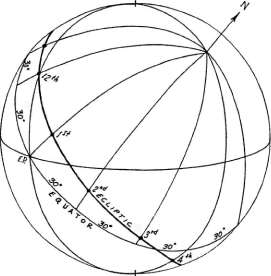 Рисунок 6-1 В Меридианной (или Зариеля) системе домов экватор делится на двенадцать 30-ти градустных дуг (начиная от RAMC) при помощи шести часовых кругов (рисунок 6-1). Точки, в которых часовые круги пересекают эклиптику, дают значение долготы куспидов домов в Меридианной системе домов. В Меридианной системе 10-й и 4-й куспиды как обычно соответствуют МС и IC, но 1-й куспид является правильной долготой точки Востока (вместо Асцендента) и 7-й куспид является правильной долготой точки Запада (вместо Десцендента). Здесь правильная долгота (RL) точки обозначает долготу пересечения эклиптики часовым кругом, проходящим через точку. |
||
| Мунданное соединение в Меридианной системе В меридианной системе две точки считаеются находящиеся
в соединении, если они обе лежат на одном и том же часовом круге ( то есть они имеют одинаковый RA).
Следовательно Меридианная Мунданная позиция является прямым восхождением и дуга дирекции
промиссора к Мунданному соединению с сигнификатором является простой разницей их значений RA.
В данной системе не существует различия между промиссором и сигнификатором, то есть прямые и
обратные дирекционные дуги равны, но противоположны по знаку. |
||
| Мунданные дирекции с произвольным аспектом в Меридианной системе Мунданные дирекции с произвольным аспектом вычисляются
путем прибавления величины аспекта (60, 90, 120 и т.д.) к RA сигнификатора и вычитания полученной
суммы из RA промиссора. |
||
| Зодиакальные дирекции и дирекции с учетом широты в Меридианной системе Зодиакальные дирекции вычисляются путем прибавления
величины аспекта к долготе промиссора, преобразованием полученной суммы в RA по формуле А2 и
вычитанием RA сигнификатора из неё. |
||
| Мунданные параллели в Меридианной системе Промиссор Р движется к мунданной параллели с сигнификатором S. Вычисление величины RA мунданно параллельной точки к сигнификатору производится по следующему алгоритму:
где MD(s) является MD сигнификатора. Тогда дуга дирекции P||S Merid
определяется уравнением: |
||
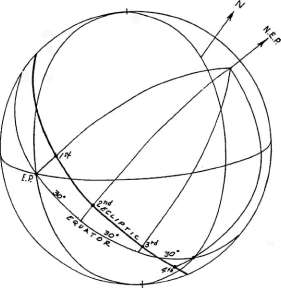 Рисунок 6-2 В системе домов Моринуса экватор
делится на двенадцать 30-ти градустных дуг (начиная от RAMC) при помощи
шести кругов долготы {большие круги, проходящие через полюса эклиптики;
полюса локализованы в точках RA=270, D = со-Е (Северный полюс)
и RA=90, D= -со-Е (Южный полюс)}. В точках , где эти круги долготы
пересекают эклиптику, находятся куспиды домов системы Моринуса (рисунок
6-2). Таким образом 10-й и 4-й куспиды домов Моринуса соответствуют долготе
RAMC и RAIC соответственно, вместо MC и IC, а 1-й и 7-й куспиды соответствуют
долготе точек Востока и Запада соответственно, вместо Асцендента и Десцендента. |
||
| Мунданное соединение в системе Моринуса 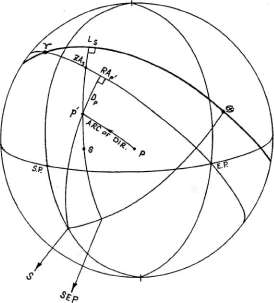 Рисунок 6-3 Для расчета дирекции промиссора Р к мунданному соединению
с сигнификатором S в системе Моринуса (рисунок 6-3) необходимо определить RA точки Р', которая лежит
на дневном круге точки Р и имеет такую же долготу, как и S. Это вычисляется из формулы А6, используя
долготу S и склонение Р. Для вычисления дуги дирекции необходимо полученную RA вычесть
из RA промиссора. |
||
| Зодиакальные дирекции и дирекции с учетом широты в системе Моринуса Рассчитаем зодиакальную дирекцию в системе Моринуса,
прибавив величину аспекта к долготе промиссора, затем находим RA точки аспекта по формуле А2
и склонение точки аспекта по формуле А4. Используя это склонение точки аспекта совместно с долготой
сигнификатора в формуле А6 вычисляем RA, затем вычитаем полученную RA из RA точки аспекта,
и получаем дугу дирекции. |
||
| Мунданные дирекции с произвольным аспектом в системе Моринуса Вычислим мунданную дирекцию с произвольным аспектом в системе Моринуса. Вначале необходимо вычислить зодиакальное восхождение сигнификатора. Зодиакальное восхождение тела вычисляется следующим образом (формула А2 здесь не используется потому что она работает с часовыми кругами, а здесь необходима формула для кругов долготы). Пусть X = Arctg(tg(L)/cos(E))
Вычислив ZA сигнификатора прибавляем к нему величину аспекта, получая таким образом ZA точки аспекта. Долготу точки аспекта получаем следующим образом. Пусть Х = Arctg(tg(ZA(ap)*cos(E))
Затем полученная долгота точки аспекта
используется совместно со склонением промиссора в формуле А6 для вычисления
RA. Для определения дуги дирекции вычисленное RA вычитается из RA промиссора. |
||
| Мунданные параллели в системе Моринуса Мунданные параллели являются наиболее интересными
в системе Моринуса, так как функцию, которую выполняет меридиан в большинстве других систем
домов, здесь выполняет большой круг, проходящий через полюса Мира, полюса эклиптики и точки
Рака и Козерога. Другими словами полушарие от Рака до Козерога можно рассматривать
как "восходящую" сторону гороскопа, а полусферу от Козерога до Рака можно рассматривать
как "заходящую" сторону (так как W тела является меньшей величиной, чем его RA при D > 0, и W
является большей величиной чем RA при D < 0, где W является зодиакальным восхождением.
Это потому что полюса эклиптики не лежат на мередиане, тогда как полюса горизонта, первого
вертикала и экватора лежат). |
||
| В Равнодомной системе домов эклиптика
делится на двенадцать 30-ти градусных дуг (обычно начиная от Асцендента).
Однако, если мы рассматриваем Равнодомную систему как проекционную систему,
нет пути для определения мунданной позиции до тех пор, пока проекционные
полюса не будут установлены. Если Равнодомную систему описывать как деление
эклиптики шестью кругами долготы, тогда две точки будут считаться находящимися
в соединении, если они имеют одинаковое значение долготы, как это описывается
в системе Моринуса. И фактически примарная дирекция, определенная на такой
манер, будет идентична такой дирекции в системе Моринуса, за исключением
мунданных дирекций с произвольным аспектом. В Равнодомной системе при
расчете мунданной дирекции с произвольным аспектом величину аспекта следует
прибавлять к долготе сигнификатора (вместо ZA сигнификатора в системе
Моринуса), и затем полученную долготу точки аспекта использовать со склонением
промиссора в формуле А6 для получения RA. Для определения дуги дирекции
вычисленное RA отнимается от RA промиссора. |
||
| В Порфирия системе домов дуга вдоль эклиптики от МС до
Асцендента делится на три равные части, точки деления дают положение куспидов 11-го и 12- домов в
Порфирия системе. Дуга вдоль эклиптики от Асцендента до IC делится на три равные части, точки деления
дают положение куспидов 2-го и 3-го домов в Порфирия системе. Как и в случае с Равнодомной
системой домов, Порфирия система может быть описана как проекционная система только после того,
как полюса проекции будут установлены, и совсем не очевидно, что эти полюса должны быть
единственными. Вопрос далее усложняется фактом, что круг, который делится (эклиптика),
должен быть разделен на не равные дуги. Первая проблема может быть решена, если мы будем
считать что полюсами проекции являются полюса эклиптики, так что мунданное соединение
(а также зодиакальные и с учетом широты дирекции) в Порфирия системе будет совпадать с тем,
что показывает система Моринуса (хотя она может быть "Меридианная", "Кампануса", "Горизонтальная",
и так далее). Вторая проблема может быть решена введением понятия поквадрантная
Мунданная позиция.
Дирекция промиссора P к мунданному аспекту с сигнификатором S в Порфирия системе рассчитывается следующим образом. Пусть РоМР(ар) = РоМР(s) + А, где РоМР(ар) будет Порфирия Мунданноцй позицией точки аспекта (на эклиптике). Затем преобразуем РоМР(ар) снова в долготу по следующему правилу:
Затем используем эту долготу точки аспекта совместно
со склонением промиссора в формуле А6 для вычисления RA. Вычисленное RA отнимается от RA
промиссора, определяя дугу дирекции P A S Porph mund. |
||
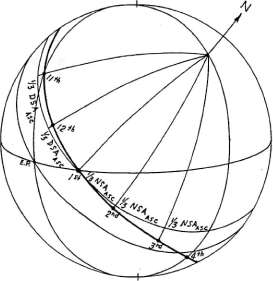
Рисунок 6-4 В Алкабитусе системе (рисунок 6-4) 11-й и 12-й куспиды домов
определяются при делении на три равные части дневной полудуги Асцендента и проекцией точек
деления на эклиптику при помощи часовых кругов. Куспиды 2-го и 3-го домов определяются
аналогичным образом при деление на три равные части ночной полудуги Асцендента. Западные
куспиды домов определяются делением на три равные части соответствующих полудуг Десцендента.
Две точки считаются находящимися в соединении Алкабитуса системе, если они лежат на одном и том
же часовом круге (имеют одинаковую RA), и поэтому примарная дирекция в Алкабитуса системе
является аналогичной той, которая используется в Меридианной системе, за исключением
мунданной дирекции с произвольным аспектом. Алкабитуса мунданная дирекция с произвольным
аспектом может быть определена тем же путем, как и в Меридианной системе, но с учетом поквадранной
Мунданной позиции, как в Порфирия системе.
Тогда дирекция промиссора Р к мунданному аспекту А с сигнификатором S в Алкабитуса системе определяется следующим образом. Пусть АМР(ар) = АМР(s)+ А, где АМР(ар) является Алкабитум Мунданной позицией точки аспекта сигнификатора. Преобразуем АМР(ар) в RA:
Для определения дуги дирекции P A
S Ale mund величина RA(ap) точки аспекта к сигнификатору вычитается из
RA промиссора. |
||
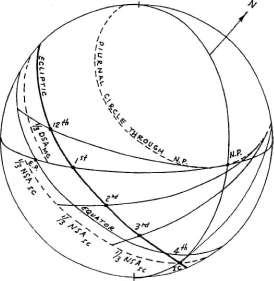
Рисунок 6-5 В системе домов Коха или Домов места
рождения (рисунок 6-5) дневные полудуги Мс делятся на три равные части
и точки деления проецируются на эклиптику при помощи кругов восхождения.
Круги восхождения являются большими кругами, которые проходят касательно
к дневным кругам точек Севера и Юга на горизонте. Каждая точка небесной
сферы со склонением меньшим, чем со-широта места рождения лежит
на двух таких кругах - один круг восхождения (круг горизонта на момент
восхода точки) и другой круг захождения (круг горизонта на момент точки
захода). Таким образом N-й куспид дома Коха является точкой на эклиптике,
имеющей такое же наклонное восхождение (или захождение, если находится
западнее меридиана) как и точка, RA которой и склонение определяются уравнениями:
|
||
| Мунданное соединение в системе Коха Две точки считаются находящимися в соединении в системе Коха,
если они лежат на одном и том же круге склонения, то есть они имеют одинаковое наклонное восхождение
(если находятся к востоку от меридиана) или одинаковое наклонное захождение (если с запада от меридиана).
Рассмотрим дирекцию промиссора Р к мунданному соединению с сигнификатором S.
Точка на дневном круге промиссора, которая имеет такое же ОА как и S должна иметь: |
||
| Зодиакальные дирекции в системе Коха В зодиакальной дирекции Коха величина
аспекта прибавляется к долготе промиссора. Величины RA и склонение для
этой точки находятся соответственно по формулам А2 и А4. Склонение используется
в формуле 1-1 для нахождения разницы восхождений точки аспекта, а величины
RA и AD точки аспекта используются в формулах 2-1 и 2-2 для нахождения
OA или OD точки аспекта (в зависимости от того, с восточной или западной
стороны меридиана находится сигнификатор). Затем OA или OD сигнификатора
вычитается из ОА или OD точки аспекта, для нахождения дуги дирекции. Зодиакальные
дирекции Коха, вычисленные таким образом, также называют "Johndro" дирекции. |
||
| Дирекции с учетом широты в системе Коха При вычислении дирекции с учетом широты в системе Коха
величина аспекта прибавляется к долготе промиссора для нахождения точки аспекта.
Затем эта долгота используется совместно с широтой тела на момент аспекта в формуле А5
для нахождения склонения и в формуле А6 для нахождения RA точки аспекта. Величина AD
точки аспекта вычисляется по формуле 1-1, а величина ОА (если сигнификатор восточнее меридиана)
или OD (если западнее) точки аспекта вычисляется из формулы 2-1 или 2-2.
Затем величина ОА (или OD) сигнификатора отнимается от ОА (или OD) точки аспекта для нахождения
дуги дирекции. |
||
| Мунданные дирекции с произвольным аспектом в системе Коха 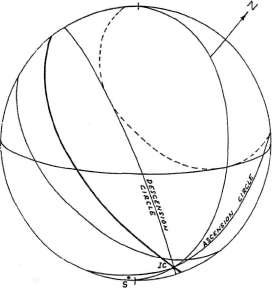
Рисунок 6-6 Мунданная дирекция с произвольным
аспектом в системе Коха может быть вычислена путем прибавления величины
аспекта к ОА (или OD) сигнификатора и вычитания полученной суммы из ОА
(или OD, если сигнификатор с западу от меридиана) промиссора, для нахождения
дуги дирекции. Однако можно также говорить, что мунданные дирекции с произвольным
аспектом в системе Коха должны рассматриваться поквадрантно (как в Порфирия
системе), хотя такое утверждение сталкивается с несколькими проблемами.
Заметьте однако, что такое определение
возможно для тела, которое лежит в Первом квадранте и имеет КМР > 90;
для тела , которое лежит во Втором квадранте и имеет КМР < 90; для тела,
которое лежит в Третьем квадранте и имеет КМР > 270; для тела, которое
лежит в Четвертом квадранте и имеет КМР < 270. Например КМР(со) = 115,57
и следовательно комета лежит в пределах пятого градуса пятого дома Коха,
даже хотя и находится восточнее меридиана.
Затем вычитаем ОА(ар) (или OD(ap)) из ОА (или OD) промиссора
(в зависимости от того, с восточной или западной стороны меридиана находится точка аспекта)
для того, чтобы получить дугу дирекции P A S Koch mund. 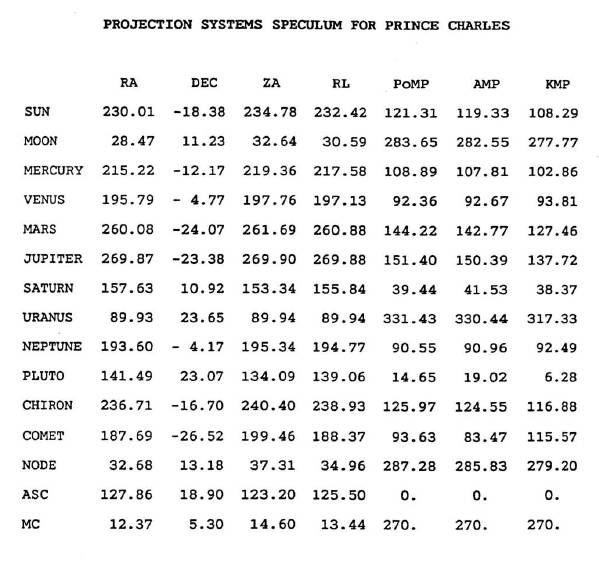 |
||
| Наверх Оглавление |
||
|
Copyright© 2004 STELLIUM.RU Webmaster |
||