Bob Makransky "Примарные дирекции"

Глава 5: Горизонтальная система домов

Горизонтальная система домов

    В горизонтальной системе домов горизонт делится на двенадцать 30 градусных дуг (начиная от точки Востока) при помощи шести вертикальных кругов (большие круги, проходящие через зенит и надир). Точки, в которых эти круги пересекают эклиптику, дают значение долготы куспидов в Горизонтальной системе домов (рисунок 5-1).
    Надо заметить, что куспиды 10-го и 4-го дома соответствуют МС и IC, как обычно, а вот куспидом 1-го дома является Антивертекс (вместо Асцендента) и куспидом 7-го дома является Вертекс (вместо Десцендента).

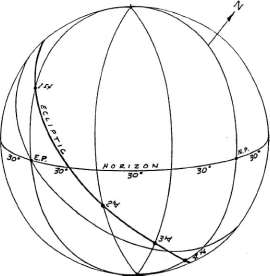Рисунок 5-1

Мунданная позиция в Горизонтальной системе

    В Горизонтальной системе домов две точки считаются находящимися в соединении (имеют одинаковую Мунданную позицию) если они лежат на одном и том же вертикальном круге. Мунданная позиция точки в Горизонтальной системе домов обозначается как EPD, и равняется дуге измеренной вдоль горизонта от точки Востока (или Запада) до пересечения с вертикальным кругом, проходящим через точку (рисунок 5-2).
    Когда Мунданная позиция точки в Горизонтальной системе отображается дугой на шкале от 0 до 360 градусов (измеренной вдоль горизонта в восточном направлении от точки Севера до пересечения с вертикальным кругом, проходящим через точку), тогда эта позиция будет называться азимутом (AZ) точки.

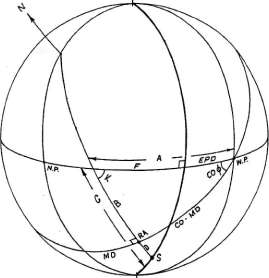Рисунок 5-2

Расстояние от точки Востока

    Вернемся к рисунку 4-4, на котором указываются десять возможных позиций локализации тела в любом выбранном квадранте. Рассмотрим Второй квадрант и случай 6, когда тело S лежит между экватором и Первым вертикалом (рисунок 5-2).
    Найдем EPD тела S, рассмотрев треугольник, сторонами которого являются дуги горизонта (= А на рисунке), часового круга через точку S (=B) и экватора (= со-MD). Назовем угол между горизонтом и часовым кругом К. Угол между горизонтом и экватором равен со-ф. Тогда имеем:
    cos(со-ф) = tg(со-MD)*ctg(A) или
    A = Arctg(ctg(MD)/sin(ф)).
    Далее: sin(со-MD) = tg(В)*ctg(со-ф) или
    В = Arctg(cos(MD)*ctg(ф)).
    Далее: cos(К) = cos(со-MD)*sin(со-ф) или
    cos(К) = sin(MD)*cos(ф).
    Рассмотрим треугольник, сторонами которого являются часовой круг через точку S (= C), горизонт (=F) и вертикальный круг через точку S. Угол между горизонтом и часовым кругом равен К, а С численно равно В - D (так как D < 0), где D является склонением S. Тогда:
    cos(К)= tg(F)*ctg(С) и заменяя cos(K) имеем:
    sin(MD)*cos(ф)= tg(F)*ctg(С) или
    F = Arctg(sin(MD)*cos(ф)*tg(C))
    Расстояние от точки Востока для тела S таким образом равно: EPD = A - F, а его азимут равен 270 + EPD (так как азимут точки Востока равен = 270).

Алгоритм вычисления EPD и азимута

    Основной алгоритм вычисления EPD и азимута для тела следующий:

1. Если MD = 0 тогда EPD = 90 и в случае
   если ф > 0 тогда:
       если MD является UMD тогда AZ=180
       если MD является LMD тогда AZ= 0.
   если ф < 0 тогда:
       если MD является UMD тогда AZ= 0
       если MD является LMD тогда AZ= 180.
2. Если MD= 90 тогда EPD = Arctg(cos(ф)*tg(D)), где D является склонением тела. В случае:
       если тело лежит в Первом или Четвертом квадрантах тогда AZ= 90- EPD;
       если тело лежит во Втором или Третьем квадранте, тогда AZ= 270 + EPD.
   Заметьте, что эта формула позволяет величине EPD иметь отрицательное значение.
3. 3. Если 0 < MD < 90 тогда:
   пусть A = Arctg(ctg(MD)/ sin|ф|)
   В = Arctg(cos(MD)*ctg|ф|)
   Далее:
   если ф > 0 тогда
       если MD является UMD тогда пусть C = B + D
       если MD является LMD тогда пусть С = B - D
   если ф < 0 тогда
       если MD является UMD тогда пусть C = B - D
       если MD является LMD тогда пусть C = B + D,
   где D является склонением тела.
4. Пусть F=Arctg(sin(MD)*cos(ф)*tg(C)) тогда EPD=|A-F|.
   Если ф > 0 тогда:
       если тело лежит в Первом или Четвертом квадрантах, тогда:
           если MD является UMD тогда AZ = 90 + A - F
           если MD является LMD тогда AZ = 90 - A + F;
       если тело лежит во Втором или Третьем квадрантах, тогда:
           если MD является UMD тогда AZ = 270 - A + F
           если MD является LMD тогда AZ = 270 + A - F.
   Если ф < 0 тогда:
       если тело лежит в Первом или Четвертом квадрантах, тогда:
           если MD является UMD тогда AZ = 90 - A + F
           если MD является LMD тогда AZ = 90 + A - F;
       если тело лежит во Втором или Четвертом квадрантах, тогда:
           если MD является UMD тогда AZ = 270 + A - F
           если MD является LMD тогда AZ = 270 - A + F.
   Заметьте, что в приведенном выше алгоритме величины C и F могут иметь отрицательные значения.

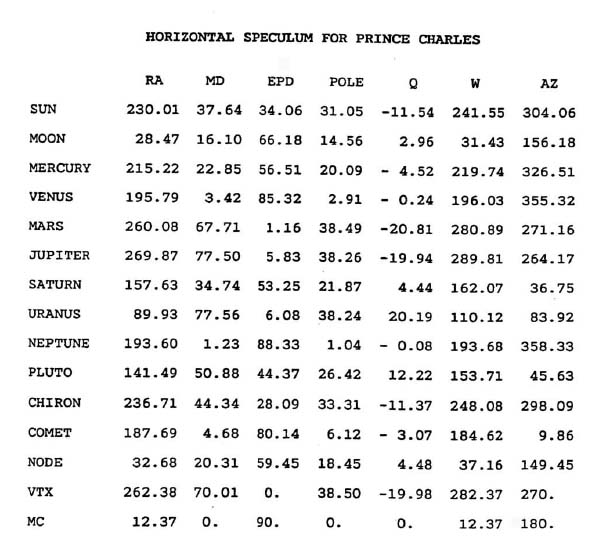
    Пример
    EPD(su):
    D(su) = -18,38; MD(su) = 37,64;
    A = 58,89; В = 32,21; С = 50,59; F = 24,83; EPD = 34,06; AZ = 304,06
    EPD(mo):
    D(mo) = 11,23; MD(mo) = 16,10;
    A = 77,27; В = 37,39; С = 48,62; F = 11,09; EPD = 66,18; AZ = 156,18

Полюс, Q и W

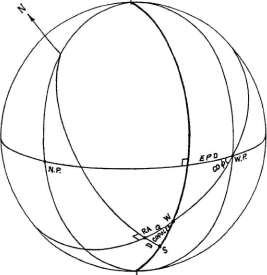Рисунок 5-3

    Когда EPD тела S будет вычислено (рисунок 5-3), его со-полюс (угол между экватором и вертикальным кругом через тело S) и полюс могут быть вычислены из треугольника, чьими сторонами являются дуги экватора, вертикального круга через точку S , и горизонта (=EPD). Угол между экватором и горизонтом равняется со-ф. Поэтому получаем:
    cos(co-полюс)= cos(EPD)*sin(co-ф) или
    формула 5-1:
    полюс = (+/-) Arcsin(cos(EPD)*cos(ф)),
    то есть полюс должен иметь такой же алгебраический знак, как и ф.
    Величина полюса изменяется от 0 (если тело находится на меридиане) до со-ф (если тело находится на первом вертикале).
    По определению Q это разница восхождений для тела под своим со-полюсом. Величина Q равняется дуге вдоль экватора от пересечения с часовым кругом, проходящим через тело, до пересечения с вертикальным кругом, проходящим через тело. Q может быть вычислено из треугольника, чьими сторонами являются дуги часового круга через тело (= D, склонение тела), вертикального круга через тело и экватора (=Q). Угол между экватором и вертикальным кругом равняется со-полюс. Поэтому получаем:
    sin(Q) = tg(D)*ctg(co-полюс) или
    формула 5-2: Q=Arcsin(tg(D)*tg(полюс))
    По определению W это наклонное захождение (восхождение) тела под своим со-полюсом. Величина W определяется точкой пересечения экватора и вертикального круга, проходящего через тело. Значение W выражается в единицах RA. Тогда:
    формула 5-3:
        если тело лежит в Первом или Четвертом квадрантах, тогда W =RA +Q
        если тело лежит во Втором или Четвертом квадрантах, тогда W = RA +Q,
        где RA является RA тела.

Мунданное соединение в Горизонтальной системе

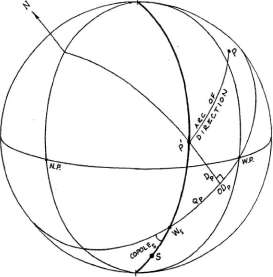Рисунок 5-4

    Промиссор может быть направлен к мунданному соединению с сигнификатором в Горизонтальной системе домов следующим образом. Рисунок 5-4 показывает сигнификатор S, находящийся во Втором квадранте и промиссор Р в Третьем квадранте. Промиссор движется благодаря вращению Небесной сферы вдоль дневного круга от своей натальной позиции в позицию Р', которая является пересечением с вертикальным кругом, проходящим через сигнификатор S. Позиция Р' рассматривается как точка соединение промиссора с сигнификатором S. RA этой точки P', обозначенное как OD(p), является наклонным захождением (восхождением) промиссора под со-полюсом сигнификатора.
    OD(p) определяется как точка, удаленная от W(s) (W сигнификатора) на расстояние дуги Q(p), являющейся разницей восхождений промиссора под со-полюсом сигнификатора. Q(p) может быть определено из треугольника чьими сторонами являются дуга экватора (=Q(p)), дуга часового круга через точки Р' и OD(p) (равная D(p), склонению промиссора) и дуга вертикального круга через сигнификатор. Угол между экватором и вертикальным кругом равняется со-полюс(s). Тогда имеем:
    sinQ(p) = tgD(p)*ctg(co-полюс(s)) или
    формула 5-4: Q(p) = Arcsin(tgD(p)*tg(полюс(s))),
    где D(p) является склонением промиссора, а полюс(s) является полюсом сигнификатора.
    На рисунке 5-4 видно, что OD(p) = W(s) + Q(p) и дуга дирекции равна RA(p) - Q(p), поэтому:
    Arc = RA(p) - (W(s) + Q(p)) = (RA(p) - Q(p)) - W(s) = W(p) - W(s).

Алгоритм расчета мунданного соединения в Горизонтальной системе

    Основной алгоритм для расчета дуги дирекции промиссора Р к мунданному соединению с сигнификатором S в Горизонтальной системе домов следующий:
    формула 5-5:
    если сигнификатор лежит в Первом или Четвертом квадрантах, тогда W(p)= RA(p) + Q(p)
    если сигнификатор лежит во Втором или Третьем квадрантах, тогда W(p)=RA(p) - Q(p),
где RA(p) является натальным RA промиссора, а Q(p) является разницей восхождений промиссора под со-полюсом сигнификатора (из формулы 5-4).
    Формула 5-6:
    Дуга дирекции промиссора Р к соединению с сигнификатором S (P CONJ S Horiz mund) дается выражением:
     Arc = W(p) - W(s),
    где W(s) является W сигнификатора (согласно правилам Горизонтальной системы).
    Дуга является положительной если дирекция прямая и отрицательной, если дирекция обратная.
    Пример: SU CONJ ME Horiz mund d:
    D(su)= -18,38; полюс(me)= 20,09;
    согласно формуле 5-4; Q(su) = -6,98; RA(su) = 230,01;
    согласно формуле 5-5; W(su) = 236,99; W(me) = 219,74;
    согласно формуле 5-6; Arc = 17,25.
    SA CONJ VE Horiz mund c:
    D(sa) = 10,92; полюс(ve) = 2,91;
    согласно формуле 5-4; Q(sa) = 0,56; RA(sa) = 157,63;
    согласно формуле 5-5; W(sa) = 157,07; W(ve)= 196,03;
    согласно формуле 5-6; Arc = -38,96.
    Заметьте, что если МС является сигнификатором, тогда W(s) = RAMC и W(p) = RA(p) (так как полюс(s) и Q(p) равны нулю), поэтому формула 5-6 принимает вид: Arc= RA(p) - RAMC.
    Также если Вертекс является сигнификатором, тогда W(s) = OD2(vtx) и полюс(s) = co-ф, следовательно Q(p) = Arcsin(tgD(p)*ctg(ф)) = AD2(р) и W(p) равно OD2(p), так что формула 5-6 принимает вид Arc = OD2(p) - OD2(vtx).

Зодиакальные дирекции в Горизонтальной системе

    Зодиакальные дирекции в Горизонтальной системе домов вычисляются обычным способом: долгота точки аспекта промиссора равна долготе промиссора плюс величина аспекта. Используя долготу точки аспекта, вычисляется RA и склонение точки аспекта по формулам А2 и А4. Далее поступаем как при расчете мунданного соединения, используя точку аспекта как промиссор.
    Пример: MO TRI SA Horiz zod c:
    трин к Луне соответствует точке 0 дева 26;
    из формулы A2; RA точки аспекта = 152,50;
    из формулы A4; склонение точки аспекта = 11,32;
    полюс(sa) = 21,87, тогда по формуле 5-4; Q(ар)=4,61;
    по формуле 5-5; W(ар)=157,11; W(sa)= 162,07;
    тогда по формуле 5-6; Arc = -4,96.

Дирекции с учетом широты (field plane) в Горизонтальной системе

    Дирекции с учетом широты вычисляются таким же образом, как и зодиакальные дирекции, но только вместо нулевого значения широты используется широта тела на момент аспекта. Рассматривается долгота и наблюдаемая на момент аспекта широта точки аспекта. Склонение и RA точки аспекта расчитываются по формулам А5 и А6. Далее поступаем как при расчете мунданного соединения, используя точку аспекта как промиссор.
    Пример: MO TRI SA Horiz с:
    определим широту, которую будет занимать Луна на момент, когда будет создан трин к Сатурну: долгота этой точки аспекта равняется 0 дева 26 и Луна достигнет этой точки 23 ноября 1948 в 19:32 GMT, имея в этот момент широту 4 N 41;
    из формулы A5; склонение точки аспекта равно 15,70;
    из формулы А6; RA(ар) = 154,22; полюс(sa) = 21,87;
    по формуле 5-4; Q(ар) = 6,48;
    по формуле 5-5; W(ар) = 160,70; W(sa) = 162,07 ;
    и по формуле 5-6; Arc = -1,37

Мунданные параллели в Горизонтальной системе

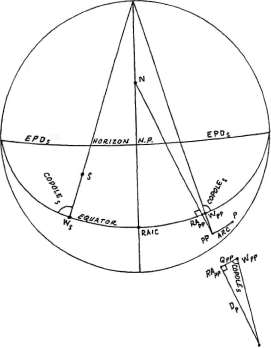
Рисунок 5-5

    В горизонтальной системе домов две точки (РР и S на рисунке 5-5, который показывает небесную сферу, спроецированную на Первый вертикал) будут находиться в мунданной параллели, если они лежат с противоположных сторон меридиана и если вертикальные круги через эти точки пересекают горизонт на одинаковом расстоянии от меридиана, то есть если EPD этих двух точек равны и измеряются от противоположных полюсов меридиана (точка Востока или Запада). Две точки находятся в Мунданной контрпараллели когда располагаются по одну сторону меридиана (но с противоположных сторон горизонта) и имеют равные значения EPD от одного и того же полюса меридиана.
    Расчитаем мунданную параллель Р||S Horiz mund, учитывая что W(pp) (W точки, муннданно параллельной сигнификатору) определяется уравнением:
    W(рр) = 2* RA - W(s),
    где RA является RA ближайшего меридиана (RAMC или RAIC) к сигнификатору и W(s) является W сигнификатора. Заметим также, что раз EPD этих точек равны, полюса S и РР также равны, так что Q(pp) параллельной точки вычисляется обычным образом из формулы 5-4:
    Q(pp) = Arcsin (tg D(p)* tg(полюс(s)), где D(p) является склонением промиссора и полюс(s) является полюсом сигнификатора. Однако, здесь Q(pp) присоединяется к W(pp) со знаком, противоположным тому, который используется при расчете соединения (так как параллельная точка лежит с противоположной стороны меридиана от сигнификатора), так что правило формулы 5-5 должно быть обращено.
    Основной алгоритм вычисления дуги дирекции промиссора Р к Мунданной параллели с сигнификатором S в Горизонтальной системе домов следующий:

1. Вычислим W(pp) параллельной точки: W(pp) = 2*RA(m) - W(s),
   где RA(m) = RAIC если MD сигнификатора является LMD и RA(m)= RAMC если MD сигнификатора является UMD, и W(s) является W сигнификатора (по правилу Горизонтальной системы).
2. Вычислим Q(pp) параллельной точки из формулы 5-4, используя D(p) промиссора и полюс(s) сигнификатора.
3. Если сигнификатор лежит в Первом или Четвертом квадрантах, тогда RA(pp) = W(pp) + Q(pp);
   если сигнификатор лежит во Втором или Третьем квадрантах, тогда RA(pp) = W(pp) - Q(pp).
4. Дуга дирекции P||S Horiz mund: равняется ARC = RA(p) - RA(pp), где RA(p) является RA промиссора.

    Для вычисления дуги дирекции промиссора Р к мунданной контрпараллели с сигнификатором S необходимо в шаге 1 заменить W(pp) = 2*RA(m) - W(s) +180 и обратить правило в шаге 3.
    Пример: SA||ME Horiz mund c:
    RAIC = 192,37; W(me) = 219,74;
    следовательно W(рр) = 165,00; D(sa) =10,92 и полюс(me) = 20,09;
    следовательно из формулы 4-4; Q(рр)= 4,05; RA(рр) =160,95; RA(sa) =157,63;
    отсюда Arc = -3,32.

Мунданные дирекции с произвольным аспектом в Горизонтальной системе

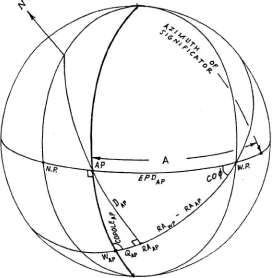
Рисунок 5-6

    Мунданные дирекции с произвольным аспектом в Горизонтальной системе домов могут быть вычислены следующим образом (рисунок 5-6): азимут точки аспекта к сигнификатору (AP, которая лежит на горизонте) равняется азимуту сигнификатора плюс А, где А является величиной аспекта (60, 90, 120 и т.д.). На рисунке 5-6 АР находится западнее меридиана, так что EPD точки АР равняется |AZ(ap) - 270|. Сейчас полюс(ар) точки аспекта может быть найден из формулы 5-1. Склонение D(ap) и RA(ap) точки аспекта вычисляются из треугольника, чьими сторонами являются дуги горизонта (=EPD(ap)), часового круга через точку аспекта (=D(ap)) и экватора (= RA(wp) - RA(ap)). Угол между горизонтом и экватором равняется со-ф, тогда получаем:
    sin(D(ap)) = sin(co-ф)*sin*(EPD(ap)) или
    D(ap) = Arcsin(cos(ф)*sin(EPD(ap))
    Далее: cos(co-ф) = tg(RA(wp) - RA(ap))* ctg(EPD(ap)) или
    RA(ap) = RAMC - 90 - Arctg(sin(ф)*tg(EPD(ap))
    Сейчас Q(ap) может быть получена из формулы 5-2 используя D(ap) и полюс(ар), а W(ap) может быть получена из формулы 5-3 используя Q(ap) и RA(ap). Отсюда процесс вычисления продолжается как для мунданного соединения, рассматривая точку аспекта АР как сигнификатор.
    Итак, основной алгоритм расчета дуги дирекции промиссора к мунданному аспекту А с сигнификатором в Горизонтальной системе домов следующий:

1. Пусть AZ(ap) = AZ(s) + A, где AZ(s) является азимутом сигнификатора и А есть значение аспекта.
   Если 0 < AZ(ap) < 180 , тогда АР находится восточнее меридиана и
       EPD(ap) = | 90 - AZ(ap) |
   Если 180 < AZ(ap) < 360 , тогда АР находится западнее меридиана и
       EPD(ap) = | 270 - AZ(ap) |
   (если AZ(ap) = 0 , тогда W(ap) = RAIC и полюс(ар) = 0;
   если AZ(ap) = 180, тогда W(ap) = RAMC и полюс(ар) = 0).
2. Используя это значение EPD(ap) по формуле 5-1 определяем полюс(ар); полученное значение полюс(ар) берём с тем же алгебраическим знаком, что и ф.
3. Пусть D(ap) = (+/-) Arcsin(cos(ф)*sin(EPD(ap)),
   то есть D(ap) > 0, когда 0 < AZ(ap) < 90 или 270 < AZ(ap) < 360
   и D(ap) < 0, когда 90 < AZ(ap) < 270.
   Используя это значение склонения вместе с полюс(ар) в формуле 5-2, получаем Q(ap).
4. Пусть Х = Arctg(sin(ф)*tg(EPD(ap))
   если 0 < AZ(ap) <= 90 тогда
       RA(ap) = RAMC + 90 + X и W(ap) = RA(ap) + Q(ap)
   если 90 < AZ(ap) < 180 тогда
       RA(ap) = RAMC + 90 - X и W(ap) = RA(ap) + Q(ap)
   если 180 < AZ(ap) <= 270 тогда
       RA(ap) = RAMC - 90 + X и W(ap) = RA(ap) - Q(ap)
   если 270 < AZ(ap) < 360 тогда
       RA(ap) = RAMC - 90 - X и W(ap) = RA(ap) - Q(ap)
5. Вычислим Q(p) промиссора из формулы 5-4, используя склонение промиссора и полюс(ар) точки аспекта.
   Если 0 < AZ(ap) < 180, тогда W(p) = RA(p) + Q(p)
   если 180 < AZ(p) < 360, тогда W(p) = RA(p) - Q(p),
   где RA(p) является RA промиссора.
6. 6. Дуга дирекции Р А S Horiz mund определяется уравнением:
   Arc = W(p) - W(ap)

    Пример: MO TRI SA Horiz mund d:
    AZ(sa)= 36,75 и A = +120*;
    следовательно AZ(ар)= 156,75; EPD(ар) = 66,75;
    из формулы 5-l: полюс(ар) = 14,23; D(ар) = -34,89;
    из формулы 5-2: Q(ар)= -10,19; X= 61,23; RA(ap)= 41,14;
    W(ap)= 30,95; D(mo) = 11,23;
    следовательно по формуле 5-4: Q(mo) = 2,89; RA(mo)= 28,47;
    отсюда W(mo)= 31,36; и Arc = 0,41.
    *Заметьте, что традиционно азимут измеряют в направлении, противоположном порядку следования домов.

Copyright© 2004 STELLIUM.RU  Webmaster