Bob Makransky "Примарные дирекции"

Глава 4: Системы домов Кампануса и Региомонтануса

Мунданная позиция в проекционной системе домов.

    Имеется несколько путей для определения соединения и Мунданной позиции, фактически каждая система гороскопических домов даёт своё собственное определение Мунданной позиции и своё собственное определение примарных дирекций. Это может быть наиболее ясно проиллюстрировано в случае проекционных систем домов.
    В проекционной системе домов некоторый круг делится на двенадцать (обычно) 30 градусных дуг при помощи проекционных кругов. Круг, который делится, не обязательно должен быть большим кругом, но проекционные круги должны быть обязательно большими кругами. Двенадцать точек на эклиптике, в которых проекционные круги пересекают её, дают значение долготы двенадцати куспидам домов. В проекционной системе домов две точки считаются находящимися в соединении (имеют одинаковую мунданную позицию), если их проекции попадают в одно и тоже место на круге, который разделен на 12 частей. То есть две точки соединены, если они лежат на одном и том же проекционном круге.
    Численно Мунданная позиция точки определяется в градусах дуги, измеренной вдоль разделенного на 12 частей круга, и равна положению места пересечения данного круга с проекционным кругом, проходящим через точку.

Мунданные аспекты

    Точка считается находящейся в мунданном аспекте к сигнификатору, если дуга вдоль круга, разделенного на 12 частей, от пересечения проекционного круга с сигнификатором до пересечения проекционного круга, проходящего через точку, равняется числу градусов аспекта (60, 90, 120 и т.д.). Можно сказать, что численно Мунданная позиция аспекта точки равна численной Мунданной позиции сигнификатора плюс количество градусов в аспекте.

Система домов Кампануса

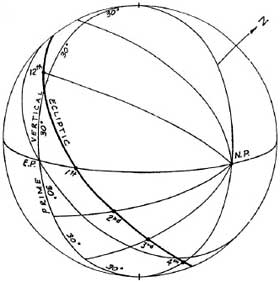Рисунок 4-1

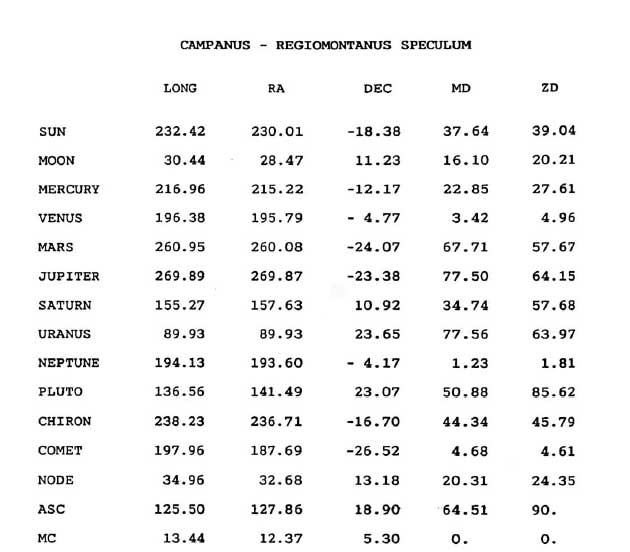
    В системе домов Кампануса (рисунок 4-1) Первый вертикал делится на двенадцать 30 градусных дуг (начиная от точки Востока) при помощи шести домовых кругов(больших кругов проходящих через точки Севера и Юга на горизонте). Точки пересечения домовых кругов с эклиптикой дают значение долготы 12 куспидов домов.

Система домов Регимонтануса

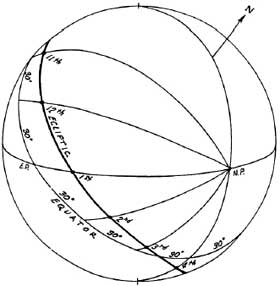Рисунок 4-2

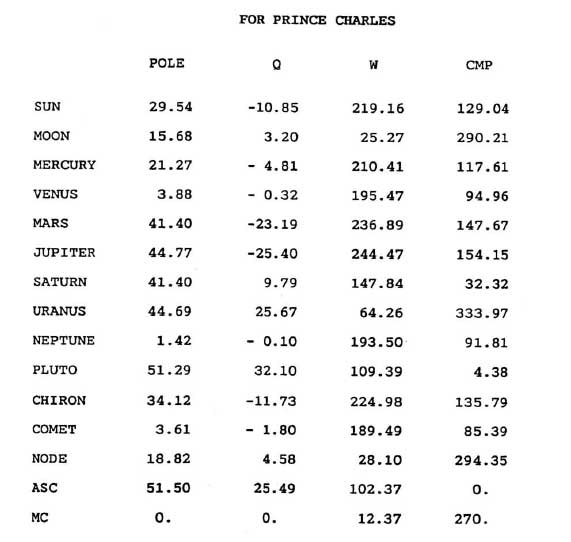
    В системе домов Регимонтануса (рисунок 4-2) небесный экватор делится на двенадцать дуг по 30 градусов каждая (начиная от точки Востока) шестью домовыми кругами. Точки пересечения домовых кругов с эклиптикой дают значение долготы 12 куспидов домов.
    В Кампануса и Регимонтануса системах, две точки считаются находящимися в соединении (или имеют одинаковую Мунданную позицию), если они лежат на одном и том же домовом круге.

Полюс и со-полюс

    Полюсом (или полярной высотой) тела S называется дуга, начинающаяся от северного (южного) Полюса мира и перпендикулярная домовому кругу, проходящему через точку S. Величина полюса изменяется от нуля (для тела лежащего на меридиане), до ф (для тела лежащего на горизонте).
    Со-полюс тела S является углом между экватором и домовым кругом, проходящим через тело S. Со-полюс численно равен (90 - полюс), если ф больше нуля и (-полюс - 90), если ф меньше нуля. Величина со-полюса изменяется от 90 (для тела лежащего на меридиане), до со-ф (для тела лежащего на горизонте).

W и Q

    Точка, в которой домовой круг, проходящий через тело, пересекает экватор, называется наклонным восхождением (захождением) тела под его собственным полюсом (W). Имеется в виду ОА (наклонное восхождение) под собственным полюсом, когда тело лежит восточнее меридиана и OD (наклонное захождение) под собственным полюсом, когда тело лежит западнее меридиана. Наклонное восхождение или захождение под собственным полюсом в системе Регимонтануса численно равно Мунданной позиции тела.
    Разница между RA и W тела называется разницей восхождений под собственным полюсом (Q).
    Из треугольника на рисунка 4-4 можно написать формулу:
    sin(Q) = tg(D)*ctg(co-полюс) или
    Формула 4-1:
    Q = Arcsin (tg(D)*tg(полюс)),
    где D является склонением тела.
    Q имеет отрицательное значение, когда склонение и полюс имеют противоположные знаки.
    Q(p) промиссора под полюсом сигнификатора является дугой вдоль экватора между W сигнификатора и RA пересечения проекционного круга проходящего через сигнификатор и дневной круг промиссора.

Зенитное расстояние

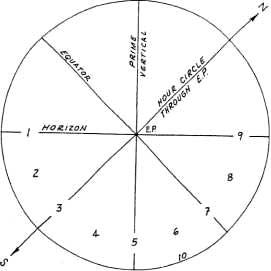Рисунок 4-3

    Перед вычислением полюса тела необходимо сначала определить его зенитное расстояние (ZD), которое равняется дуге, измеренной вдоль Первого вертикала от зенита (или надира) до точки пересечения с домовым кругом, проходящим через тело. Или другими словами, ZD является углом между меридианом и домовым кругом, проходящим через тело. Если рассматривать шкалу от 0 до 360, то Зенитное расстояние в системе домов Кампануса является численным значением Мунданной позиции тела.
    На рисунке 4-3 показано, как Первый и Четвёртый квадранты небесной сферы проецируются на меридиан. На этом рисунке северный и южный полюса Мира представляют точки окружности , а точка Востока является центром этой окружности. Имеется десять возможных позиций локализации тела в Первом квадранте, а именно:

• на горизонте к югу от Первого вертикала;
• между горизонтом и часовым кругом, проходящим через точку Востока;
• на часовом круге через точку Востока;
• между часовым кругом, проходящим через точку Востока, и Первым вертикалом;
• на первом вертикале;
• между первым вертикалом и экватором;
• на экваторе;
• между экватором и северным горизонтом, (этот случай иллюстрирует рисунок 4-4);
• на горизонте севернее Первого вертикала;
• на меридиане

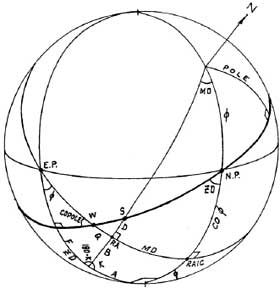Рисунок 4-4

    Рассмотрим случай 8, когда тело локализовано в точке S на рисунке 4-4. В этом случае MD = LMD, так как тело лежит на той же стороне часового круга через точку Востока, как и RAIC.
     Рассмотрим треугольник, сторонами которого являются дуги меридиана, Первого вертикала и часового круга через тело. Сторона, которая является дугой меридиана, равняется 90 + ф. Противоположный угол (между Первым вертикалом и часовым кругом) назовём К. Угол между меридианом и часовым кругом равняется MD тела. Назовем противоположную сторону (дугу Первого вертикала) А. Отсюда имеем:
    sin (90+ф) = tg(A)*ctg(MD) или
    A = Arctg (cos(ф)*tg(MD))
    Далее:
    cos(К) = cos(90+ф)*sin(MD) или
    cos(К) = -sin(ф)*sin(MD)
    Рассмотрим треугольник, сторонами которого являются дуги экватора, Первого вертикала и часового круга через тело. Сторона, которая является дугой экватора, равняется со-MD, что составляет 90 - MD. Угол между экватором и Первым вертикалом равняется ф. Противоположную сторону (дугу часового круга через тело) назовем В. Тогда имеем:
    sin(со-MD) = tg(В)*ctg(ф) или
    В = Arctg (tg(ф)*cos(MD))
    Рассмотрим треугольник, сторонами которого являются дуги Первого вертикала, часового круга через тело и домового круга через тело. Дугу часового круга от Первого вертикала до тела назовем С. Величина С численно равна В+D, где D является склонением тела. Угол между первым вертикалом и часовым кругом равняется 180-К. Дугу первого вертикала назовем F. Отсюда:
    cos (180 - K) = tg(F)*ctg(C),
    и заменяя -cos K на предыдущую формулу имеем:
    sin(ф)*sin(MD) = tg(F)*ctg(С) или
    F = Arctg (sin (ф)*sin( MD)* tg( C))
    Окончательно, зенитное расстояние (дуга Первого вертикала от Надира до пересечения с домовым кругом) равняется : ZD = A + F

Алгоритм расчета зенитного расстояния

    Алгоритм вычисления зенитного расстояния тела следующий:

1. Если MD=90 (случай 3, когда тело лежит на часовом круге, проходящем через точки Востока и Запада), тогда ZD = 90 - Arctg(sin(|ф|)*tg(D), где D - склонение тела.
   • если тело лежит в Первом или Втором квадрантах, тогда ZD измеряется от надира.
   • если тело лежит в Третьем или Четвертом квадранте, тогда ZD измеряется от зенита.
2. Если MD меньше 90 тогда
   пусть А= Arctg (cos(ф)*tg(MD))
   пусть В= Arctg (tg(|ф|)*cos(MD))
   если D и ф являются величинами одного знака, тогда:
   • если MD является UMD тогда С = В - |D|
   • если MD является LMD тогда C = B + |D|
   если D и ф являются величинами противоположных знаков, тогда:
   • если MD является UMD тогда С = В + |D|
   • если MD является LMD тогда C = B - |D|
   (если В=|D|, тогда тело может лежать точно на Первом вертикале, случай 5, в котором С и соответственно этому F равны нулю).
3. Пусть F = Arctg(sin(|ф|)*sin( MD)*tg(C))
   тогда ZD = A + F.
   Заметьте, что C и F могут быть отрицательными. Это происходит в случае 4, когда тело лежит между Первым вертикалом и часовым кругом, проходящем через точки Востока и Запада.
4. Если MD является UMD, тогда ZD измеряется от зенита.
   Если MD является LMD, тогда ZD измеряется от надира.

    Пример:
    ZD(su) : MD = 37,64; D = -18,38; A= 25,65;
    В = 44,87; С = 26,49; F = 13,39;
    ZD = 39,04 (измеренное от надира)
    ZD(mo) : MD = 16,10; D = 11,23; A = 10,19;
    В = 50,38; С= 39,15; F = 10,02;
    ZD = 20,21 (измеренное от зенита)

Алгоритмы расчета полюса, Q и W

    Обратимся к рисунку 4-4, со-полюс тела S (угол между его домовым кругом и экватором) может быть вычислен из треугольника, чьими сторонами являются дуги меридиана, экватора и домового круга через тело S. Угол между меридианом и домовым кругом равен ZD точки S. Сторона, которая является дугой меридиана (от горизонта до экватора) равняется со-ф. Противоположный ей угол (между домовым кругом и экватором) является co-полюс. Отсюда:
    cos(co-полюс) = cos(со-ф)*sin(ZD) или
    Формула 4-2:
    полюс = Arcsin(sin(ф)*sin(ZD))
    Заметим, что полюс имеет такой же алгебраический знак, как и ф.
    Разница восхождений тела под собственным полюсом (Q) может сейчас быть вычислена из
формулы 4-1, которая дается выражением: Q = Arcsin (tg(D)*tg(полюс)).
    Тогда наклонное восхождение (захождение) тела под собственным полюсом (W) вычисляется следующим образом:
    Формула 4-3:

• если тело лежит в Первом или Четвертом квадранте,
  тогда OA под собственным полюсом будет равно W = RA - Q;
• если тело лежит во Втором или Третьем квадранте,
  тогда OD под собственным полюсом будет равно W = RA + Q

Мунданное соединение в системах Кампануса и Регимонтануса

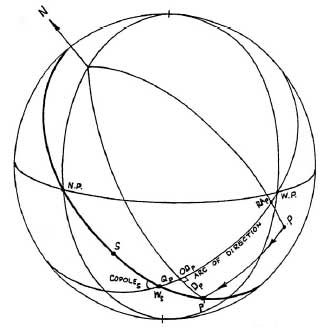
Рисунок 4-5

    Промиссор может быть направлен к мунданному соединению с сигнификатором следующим образом. На рисунке 4-5 показан сигнификатор S и промиссор Р, находящиеся во Втором квадранте. Промиссор движется, благодаря вращению небесной сферы, вдоль своего дневного круга от своей натальной позиции Р в положение P', образованное пересечением с домовым кругом, проходящим через сигнификатор S. Таким образом, в положении P' промиссор будет находиться в соединении с сигнификатором S.
    Определение: прямое восхождение P' определяет наклонное захождение (или восхождение, если сигнификатор находится восточнее меридиана) промиссора под полюсом сигнификатора OD(p).
    Разница между OD(p) и натальным RA тела Р определяет дугу дирекции P CONJ S C-R mund.
    Пусть W(s) будет W сигнификатора, как это определяется в системах Кампануса и Регимонтануса. Дуга Q(р) будет равна разнице восхождений промиссора под полюсом сигнификатора, то есть дуге вдоль экватора от W(s) до OD(p). Отсюда:
    sin(Q(p)) = tg(D(p))*ctg(со-полюс(s)) или
    Формула 4-4:
    Q(p) = Arcsin(tg(D(p))*tg(полюс(s)))
    где D(p) - склонение промиссора, а полюс(s) - полюс сигнификатора.
    Пример из рисунка 4-5:
    OD(p) = W(s) - Q(p)  ( Q(p) < О так как D(p) < 0 ) и W(s) = RA(s) + Q(s)
    следовательно OD(p) = RA(s) + Q(s) - Q(p)
    Дуга дирекции будет равна RA(p) - OD(p) или
     = (RA(p) + Q(p)) - (RA(s) + Q(s)) = W(p) - W(s)
     где W(p) является значением W промиссора, которое определяется как RA(p) + Q(p).

Алгоритм расчета Мунданного соединения в системах Кампануса и Pегимонтануса

    Основной алгоритм расчета дирекционной дуги соединения промиссора Р с сигнификатором S в системах Кампануса и Регимонтануса следующий:
    Формула 4-5:
    Если сигнификатор лежит в Первом или Четвертом квадранте, тогда W промиссора является
    W(p) = RA(p) - Q(p).
    Если сигнификатор лежит во Втором или Третьем квадрантах, то тогда W промиссора является
    W(p) = RA(p) + Q(p),
    где RA(p) - натальное RA промиссора, а Q(p) - разница восхождений промиссора под полюсом сигнификатора, которое определяется по формуле 4-4
    Q(р) = Arcsin (tg D(p)*tg(полюс(s)).
    Заметьте, что формула для W(p) полностью зависит от того, с восточной или западной стороны меридиана находится сигнификатор, вне зависимости от положения промиссора.
    Формула 4-6:
    Дуга дирекции соединения промиссора Р и сигнификатора S (P CONJ S C-R mund) определяется формулой:
    Arc = W(р) - W(s).
    Дуга имеет положительное значение в прямой дирекции и отрицательное в обратной дирекции.
   Пример:
   SU CONJ ME C-R mund d: D(su) = -18,38;
   полюс(me) = 21,27;
   по формуле 4-4: Q(su) = -7,43; RA(su) = 230,01;
   по формуле 4-5: W(su) = 222,58; W(me) = 210,41;
   по формуле 4-6: Arc = 12,17;
   SA CONJ VE C-R mund c: D(sa) = 10,92;
   полюс(ve) = 3,88;
   по формуле 4-4: Q(sa) = 0,75; RA(sa) =157,63;
   по формуле 4-5, W(sa) = 158,38; W(ve) = 195,47;
   по формуле 4-6, Arc = -37,09.
   Заметьте, что если MC является сигнификатором, то полюс(s) = 0. Следовательно Q(p) = 0 и W(p) = RA(p). Также W(s) в этом случае равняется RAMC, так что формула 4-6 принимает вид
    Arc = RA(р) - RAMC.
   Аналогично, если Асцендент является сигнификатором, то полюс(s)= ф. Следовательно W(р) = OA(р). Также W(s) в данном случае равняется ОА(asc), так что формула 4-6 принимает вид
    Arc = OA(р) - ОА(asc).

Зодиакальные дирекции в системах Кампануса и Регимонтануса

    Долгота точки аспекта промиссора равняется долготе промиссора плюс значение аспекта (+60, 90, 120 и т.д.). Из значения долготы точки аспекта вычисляется RA и склонение точки аспекта по формулам А2 и А4. Когда говорят о Мунданном соединении, имеют в виду точку аспекта, как промиссор. Поэтому дальнейшие вычисления проводятся таким же образом, как и при расчете Мунданного соединения точки аспекта с сигнификатором.
    Пример:
    MO TRI SA C-R zod c: трин к Луне попадает в 0 Дева 26 (точка аспекта);
    из формулы A2: RA этой точки = 152,50;
    из формулы A4:склонение этой точки = 11,32;
    полюс(sa) = 41,40;
    тогда по формуле 4-4: Q точки аспекта Q(ap) = 10,16;
    по формуле 4-5: W(ap) = 142,34; W(sa) = 147,84;
    тогда по формуле 4-6: Arc = -5,50

Дирекции с учетом широты (field plane directions) в системах Кампануса и Регимонтануса

    При вычислении дирекции с учетом широты, берется во внимание натальная долгота точки аспекта промиссора и широта промиссора на момент возникновения аспекта. Согласно формулам A5 и А6 вычисляется RA и склонение точки аспекта. Здесь под Мунданным соединением имеется в виду соединение с точной аспекта, как промиссором.
    Пример: MO TRI SA C-R с:
    Здесь требуется найти следующий трин Луны, с учетом её долготы, к натальной долготе Сатурна:
    долгота точки аспекта 0 Дева 26;
    Луна прибывает в эту точку 23 ноября 1948 года в 19:32 GMT, и имеет в этот момент широту 4 N 41;
    обратившись к формуле А5 и используя L = 150,44 и В = 4,68 получаем: склонение =15,70;
    из формулы А6 имеем: RA = 154,22;
    полюс(sa) = 41,40;
    тогда по формуле 4-4:Q(ap) = 14,35;
    по формуле 4-5: W(ap) = 139,87; W(sa) = 147,84;
    по формуле 4-6: Arc = -7,97

Мунданные параллели в системах Кампануса и Регимонтануса

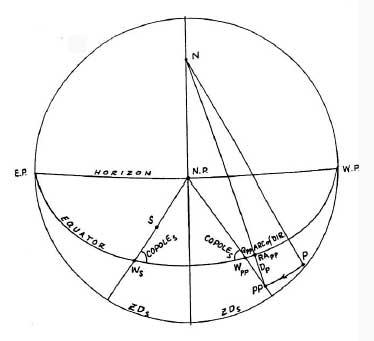
Рисунок 4-6

    В системах Кампануса и Регимонтануса две точки (РР и S на фигуре 4-6, который показывает небесную сферу, спроектированную на Первый вертикал) находятся в Мунданной параллели (ll), если они лежат с противоположных сторон меридиана и их соответствующие домовые круги пересекают Первый вертикал на одинаковом расстоянии от меридиана, то есть если их дуги ZD равны ( и измерены от одного и того же полюса горизонта - зенита или надира).
    Мунданная контрпараллель (ff) соответствует ситуации, когда две точки находятся с одной стороны меридиана и имеют одинаковые дуги ZD от противоположных полюсов горизонта.
    Таким образом, Мунданную параллель можно рассматривать как отражение Мунданного соединения через меридиан, а Мунданную контрпараллель можно рассматривать как отражение мунданной оппозиции через меридиан.
    Вычислим Мунданную параллель P || S C-R mund.
    Значение W(pp) (W мунданно параллельной точки к сигнификатору) определяется формулой:
    Формула 4-6:
    W(pp) = 2*RA(m) - W(s), где RA(m) есть RA самого близкого меридиана (RAMC или RAIC) к сигнификатору, а W(s) есть W сигнификатора. Заметьте так же, что так как ZD сигнификатора и ZD параллельной точки равны, полюса S и PP равны, так что Q(рр) параллельной точки вычисляется по обычным путем по формуле 4-4:
    Q(рр) = Arcsin (tg(D(р))*tg(полюс(s)),
    где D(p) является склонением промиссора, а полюс(s) является полюсом сигнификатора. Однако, здесь Q(pp) зависит от W(pp) в обратном направлении, чем это было бы, если бы мы рассматривали их соединение {поскольку параллельная точка лежит на противоположной стороне меридиана, по отношению к сигнификатору, то правило формулы 4-5 должно быть обращено}
    Основной алгоритм расчета дирекции промиссора Р к Мунданной параллели с сигнификатором S в системах Кампануса и Регимонтануса следующий:

1. Вычисляем W(pp) параллельной точки:
   W(pp)= 2*RA - W(s),
   где RA = RAIC, если MD сигнификатора является LMD, и RA = RAMC, если MD сигнификатора является UMD, а W(s) является W сигнификатора (согласно системам Кампануса и Регимонтануса).
2. Вычисляем Q(pp) параллельной точки из формулы 4-4, используя D(p) промиссора и Полюс(s) сигнификатора.
3. Если сигнификатор лежит в Первом или Четвертом квадрантах, тогда RA(pp) = W(pp) - Q(pp)
   Если сигнификатор лежит во Втором или Третьем квадрантах, тогда RA(pp) = W(pp) + Q(pp)
4. Дуга дирекции P||S C-R mund: определяется уравнением:
   Arc = RA(p) - RA(pp)
   где RA(p) является RA промиссора.

    Для вычисления дирекции промиссора Р к Мунданной контрпараллели с сигнификатором S в системах Кампануса и Регимонтануса, необходимо в шаге 1 записать:
    W(pp)= 2*RA - W(s) +180,
    и в шаге 3 обернуть правила расчета RA(pp).

    Пример:
    SA||ME C-R mund c:
    RAIC=192,37; W(me) =210,41;
    следовательно W(pp) = 174,33;
    D(sa)= 10,92 и полюс(me)= 21,27;
    следовательно из формулы 4-4: Q(pp)= 4,31;
    RA(pp)= 178,64; RA(sa)=157,63;
    следовательно Arc = -21,01

Мунданные дирекции при произвольном аспекте

    В мунданной дирекции с произвольным аспектом промиссор движется вдоль своего дневного круга до тех пор, пока не пересечёт домовой круг мунданного аспекта сигнификатора, в точке, от которой будет создавать аспект к сигнификатору.
     Мунданные аспекты (отличные от соединения и оппозиции) различаются в системах Кампануса и Регимонтануса, так как вычисление численной Мунданной позиции различается в этих двух системах (ZD соответствует MP Кампануса, а W соответствует МР Регимонтануса).

Мунданные дирекции при произвольном аспекте в системе Регимонтануса

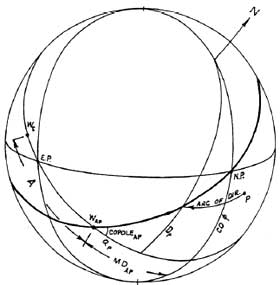
Рисунок 4-7

    Вычислим Мунданные дирекции при произвольном аспекте в системе Регимонтануса.
    Пусть W(ap) = W(s)+ A, где W(ap) является W точки аспекта (на экваторе), а А является величиной данного аспекта (60, 90, 120 и т. д.). Чтобы вычислить Q(p) нужно вначале определить Полюс точки аспекта. Обратимся к рисунку 4-7, со-полюс может быть вычислен из треугольника, сторонами которого являются дуги домового круга через точку W(ap), экватора (= MD точки W(ap)) и меридиана (= со-ф). Отсюда:
    sin(MD(ap) = tg(со-ф)*ctg(со-полюс(ap) или
    полюс(ap) = Arctg(tg(ф)*sin(MD(ap)))
    Формула 4-4:
    Q(р) = Arcsin(tg(D(p))*tg(полюс(ар))),
    где D(p) склонение промиссора.
    Отсюда W(p) вычисляется из формулы 4-5, используя RA промиссора, а дуга дирекции вычисляется из формулы 4-6, используя W(p) промиссора и W(ap) точки аспекта.
    Основной алгоритм расчета дирекции промиссора P к Мунданному аспекту А с сигнификатором S в системе Регимонтануса следующий:

1. Пусть W(ap) = W(s) + A, где W(s) является W сигнификатора (по правилу Кампануса и Регимонтануса систем), а А является величиной аспекта.
2. Пусть MD(ap) = |W(ap) - RA(m)|, где RA(m) является RA меридиана, ближайшего к точке аспекта (RAMC или RAIC).
3. Вычислим Q(p) из формулы 4-4 используя D(p) промиссора, но заменяя в формуле полюс(s) на полюс(ар), равный Arctg(tg(ф)*sin(MD(ap))).
4. Используя это значение Q(p) вместе с RA(p) промиссора по формуле 4-5 определяем W(p) (вычитая, если W(ap) находится с восточной стороны меридиана и прибавляя, если W(ap) находится с западной стороны меридиана).
5. Дуга дирекции P A S Regio mund определяется формулой: Arc = W(p) - W(ap).

    Пример: MO TRI SA Regio mund c:
    W(sa) = 147,84; A = -120;
    следовательно W(ap) = 27,84;
    RAMC = 12,37;
    следовательно MD(ap) = 15,47 и
    полюс(ар) = 18,54;
    D(mo) = 11,23;
    следовательно по формуле 4-4 Q(mo) = 3,82; RA(mo) = 28,47 и W(ар) находится восточнее меридиана, следовательно по формуле 4-5 W(mo) = 24,65; Arc = -3,19

Мунданные дирекции при произвольном аспекте в системе Кампануса

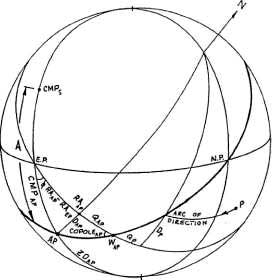
Рисунок 4-8

    Рассчитаем Мунданные дирекции при произвольном аспекте в системе Кампануса. Удобно выражать Мунданные позиции Кампануса (CMP) сигнификатора на шкале от 0 до 360 градусов, измеренную вдоль Первого вертикала от точки Востока в направлении надира.
    Пусть СМР будет Мунданной позиции Кампануса для сигнификатора и пусть ZD будет её зенитным расстоянием.
    Если сигнификатор лежит в Первом или Четвертом квадрантах, тогда:
    если ZD было измерено от зенита, тогда CMP = 270 + ZD
    если ZD было измерено от надира, тогда CMP = 90 - ZD
    Если сигнификатор лежит во Втором или Третьем квадрантах, тогда:
    если ZD было измерено от зенита, тогда CMP = 270 - ZD
    если ZD было измерено от надира, тогда CMP = 90 + ZD.
    Рассмотрим дирекцию промиссора Р к мунданному аспекту А от сигнификатора S в системе Кампануса (рисунок 4-8). СМР(ар) точки аспекта к сигнификатору (которая лежит на Первом вертикале) равняется:
СМР(s) + A, где СМР(s) является Мунданной позицией Кампануса для сигнификатора, а А является значением величины аспекта. ZD(ap) точки аспекта равно (90 - СМР(ар)).
    Полюс(ар) точки аспекта находится из формулы 4-2. Склонение и RA точки аспекта вычисляется из треугольника, чьими сторонами являются дуги Первого вертикала (=СМР(ар)), часового круга через точку аспекта (=D(ap)) и экватора (=RA(ap) - RA(ep)). Угол между Первым вертикалом и экватором равен ф, следовательно:
    sin(-D(ap)) = sin(ф)*sin(CMP(ap)), так как D(ap) < 0;
    или D(ap) = -Arcsin(sin(ф)*sin(CMP(ap)).
    Далее:
    cos(ф) = tg(RA(ap) - RA(ep))*ctg(CMP(ap)), или
    RA(ap) = RAMC + 90 + Arctg(cos(ф)*tg(СМР(ap))
    Сейчас Q(ap) может быть получена из формулы 4-1, используя D(ap) и полюс(ар), а W(ap) может быть получено из формулы 4-3, используя Q(ap) и RA(ap).
    Отсюда процесс расчета будет продолжаться как для Мунданного соединения, рассматривая при этом точку аспекта сигнификатором.
    Основной алгоритм расчета дирекции промисcора Р к мунданному аспекту А от сигнификатора в системе Кампануса следующий:

1. Пусть СМР(ар) = СМР(s) + A, где СМР(s) является Мунданной позицией Кампануса для сигнификатора (согласно правилу систем Кампануса и Регимонтануса), а А является величиной аспекта.
2. Пусть ZD(ap) = |CMP(ap) - 90| будет ZD точки аспекта. Далее используйте это значение ZD в формуле 4-2 для нахождения полюс(ар); однако берите полюс(ар) с таким же алгебраическим знаком, как и ф.
3. Пусть D(ap)= -Arcsin(sin(ф)*sin(CMP(ap)) будет склонением точки аспекта. Далее используйте это значение склонения вместе с полюс(ар) в формуле 4-1 для нахождения Q(ap).
4. Пусть X =Arctg(cos(ф)*tg(CMP(ap))
5. Если 0 < = CMP(ap) < 90 или 270 < CMP(ap) < = 360*, тогда:
       пусть RA(ap) = RAMC + 90 + X и пусть W(ap) = RA(ap) - Q(ap)
   Если 90 < CMP(ap) < 270 тогда:
       пусть RA(ap) = RAMC - 90 + X и пусть W(ap) = RA(ap) + Q(ap)
   * если СМР(ар) = 90 или 270, тогда дирекция будет направлена на IC или MC.
6. Посчитаем Q(p) из формулы 4-4 используя склонение промиссора и полюс(ар) точки аспекта.
   Если 0 < = CMP(ap) < 90 или 270 < CMP(ap) < = 360 тогда:
       пусть W(p) = RA(p) - Q(p)
   Если 90 < CMP(ap) < 270 тогда:
       пусть W(p) = RA(p) + Q(p),
   где RA(p) является RA промиссора.
7. Дуга дирекции P A S Camp mund определяется уравнением: Arc = W(p) - W(ap).

    Пример: M0 TRI SA Camp mund d: CMP(sa) = 32,32 и A = -120;
    следовательно CMP(ap) = 272,32; ZD(ap) = 182,32;
    из формулы 4-2: полюс(ар) = 1,82 (берём абсолютную величину полюса, потому что ф > 0);
    D(ap) = 51,44;
    из формулы 4-1: Q(ар) = 2,28; X = -86,28;
    RA(ар) = 16,09 и W(ар) = 13,81;
    D(mo) = 11,23;
    следовательно из формулы 4-4: Q(mo) = 0,36;
    RA(mo) = 28,47;
    следовательно W(mo) = 28,11, и Arc = 14,30.

Вовлеченные параллели (rapt parallels)

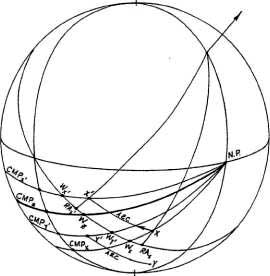
Рисунок 4-9

    Существуют неисчислимое количество возможностей и комбинаций для вычисления примарных дирекций, которые используют мунданные и зодиакальные миндпоинты, из которых только одна будет рассмотрена здесь.
    Когда мунданный миндпоинт двух тел X и Y занимает натальную Мунданную позицию третьего тела Z, тогда говорят, что X и Y находятся во вовлеченной параллели по отношению к Z, что записывается как X/Y=Z.
    В системах Кампануса и Регимонтануса вычисление дуги дирекции, по которой промиссоры X и Y должны двигаться вдоль их соответствующих дневных кругов, достигая позиций мунданно равноудаленных от натальной Мунданной позиции сигнификатора Z, является довольно сложной задачей, потому что приходится преобразовывать координаты промиссоров. Не так просто передвигать точку (МР(х) + МР(у))/2 вдоль собственных дневных кругов промиссоров к позиции MP(z); предпочтительнее, чтобы экваториальное движение X и Y было спроецировано на Первый вертикал, а затем обратно на экватор. Этот метод будет просто описан здесь.

1. Рассчитаем МР(z), численную Мунданную позицию сигнификатора (соответственно CMP(z) если система Кампануса и W(z) если система Регимонтануса).
2. Пусть начальное значение дуги дирекции будет равно: Arc = (RA(x) + RA(y))/2 - RA(z).
3. Пусть RA(x1) = RA(x) - Arc; и пусть D(x1)=D(x)
   Пусть RA(y1) = RA(y) - Arc; и пусть D(y1)=D(y)
   и тогда используя эти значения RA и склонения рассчитаем численные Мунданные позиции MP(x1) и МР(у1) в данной системе домов.
4. Поскольку Х движется по своему дневному кругу к Х1 (рисунок4-9), RA(x) движется к RA(x1) и MP(x) движется к МР(х1). Теперь мунданная позиция Х1 и Y1 отличаются от Мунданной позиции Z на дугу, длинною dMP = (MP(x1)+MP(y1))/2 - MP(z), и приращение дуги в RA, которое соответствует приращению в МР, описывается выражением:
   dArc=dMP*(RA(x)-RA(x1)/(MP(x)-MP(x1)).

    Далее, переходя к шагу 3 и заменяя значение Arc на полученное значение Arc+dArc, снова производим расчеты. Продолжаем повторять шаги 3 и 4 до тех пор, пока повторения не начнут показывать одинаковые результаты.
    Этот метод может использоваться для вычисления вовлеченных параллелей в любой системе домов, при использовании MP и числовой Мунданной позиции для данной системы домов.
    Пример:
    SU/JU = ME Camp d: Arc=28,72
    SU/JU = ME Regio d: Arc=30,37
    MO/UR = SU Camp d: Arc=3,37
    MO/UR = SU Regio d: Arc=7,38

Copyright© 2004 STELLIUM.RU  Webmaster