Bob Makransky "Примарные дирекции"

Глава 1: Введение в теорию небесной сферы

Сферические треугольники

     Большой круг на сфере является местом пересечения сферы с плоскостью, проходящей через центр сферы. Полюсами большого круга являются две точки, в которых сфера пересекается линией, проходящей через центр сферы перпендикулярно плоскости большого круга. Любой большой круг, проходящий через полюса другого большого круга, пересекает этот второй круг под прямым углом.
    Большой круг полностью определяется двумя параметрами: точкой, в которой он пересекает экватор, которая обозначается как "W", и углом, под которым он пересекает экватор, который обозначается как "со-полюс". Малый круг является пересечением сферы плоскостью, не проходящей через центр сферы. Сферический треугольник является поверхностью сферы, ограниченной тремя дугами больших кругов, пересекающимися в трех точках. Заметьте, что дуги должны образовываться большими кругами.
    Стороны сферического треугольника, так же как и его углы, измеряются в градусах, поскольку они являются дугами больших кругов. Мерой дуги является угол, созданный линиями, проведёнными из конечных точек дуги к центру сферы. Если хотя бы один угол сферического треугольника равен 90 градусам, то такой треугольник называется прямоугольным.

Небесная сфера

    Небесная сфера является сферой бесконечного радиуса, центром которого является центр Земли. Планетарные и звездные тела распределены как точки на поверхности этой сферы. Наблюдателю на Земле астрономическая сфера кажется вращающейся, планеты и звезды последовательно восходят, достигают высшей точки, и заходят. Это дневное движение планет и звезд - основание для построения первичной системы предсказаний, известной как примарные (первичные) дирекции.
    Горизонт является большим кругом, который разрезает небесную сферу плоскостью, проходящей через центр Земли. Эта плоскость параллельна поверхности, проходящей через точку в которой находится наблюдатель на поверхности Земли (точнее таких поверхностей будет две, если учитывать радиус Земли). Поэтому чтобы исключить такую двойственность, радиус Земли в теории небесной сферы принимается равным нулю. Зенит является точкой, которая находится выше головы наблюдателя. Зенит определяется местом пересечения линии, проходящей перпендикулярно горизонту через наблюдателя, с небесной сферой. Надир является точкой небесной сферы, диаметрально противоположной Зениту. Таким образом Зенит и Надир являются полюсами горизонтального круга (рисунок 1-2).

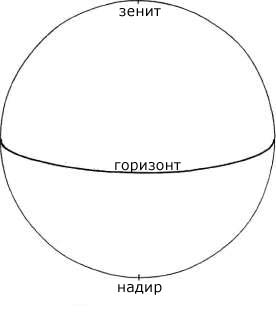Рисунок 1-2

    Небесный экватор находится на плоскости, которая проходит через земной экватор и пересекает небесную сферу. То есть небесный экватор является большим кругом, полюсами которого являются северный и южный полюса Мира. Северный полюс Мира является точкой, в которой небесная сфера пересекается осью вращения Земли. Южный полюс Мира является точкой, диаметрально противоположной северному полюсу Мира. В настоящее время северный полюс мира находится около Полярной звезды.
    Дуга от горизонта до северного полюса Мира равняется земной широте наблюдателя и обозначается как ф . Угол между горизонтом и небесным экватором дополняет земную широту наблюдателя до 90 градусов и обозначается как со-ф, то есть он численно равняется 90 минус земная широта наблюдателя. Рисунок 1-3 отображает ситуацию, когда наблюдатель находится приблизительно на 50 градусов северной широты.

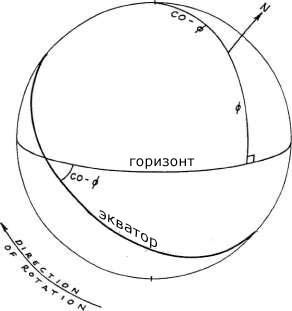Рисунок 1-3

*Северный полюс Мира (N) можно найти по правилу "левой руки". Если направление пальцев левой руки показывают направление вращения Земли, то большой палец указывает на северный полюс Мира.

Географическая и геоцентрическая широта

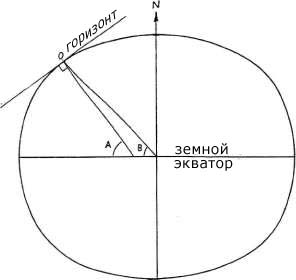Рисунок 1-4

    Существует два значения земной широты, которые могут применяться при расчете примарных дирекций (рисунок 1-4). Первое является географической широтой места на поверхности Земли, которое указывается в географических картах, равное углу образованному плоскостью экватора и линией, перпендикулярной горизонту наблюдателя в этом месте (А).
    Второе это геоцентрическая широта места на поверхности Земли равняется углу, образованному плоскостью экватора и линией, проходящей через центр Земли и локального наблюдателя в этом месте. Так как Земля является сфероидом, а не правильной сферой, эти два значения широты могут отличаться (до 12' дуги). Геоцентрическая широта может быть вычислена из географической широты по следующей формуле:
    Геоцентрическая = Arctg(0,9933*tg(Географическая)).
    Например:
    51N 30 географической широты соответствуют 51 N 18 геоцентрической широте.
    Географическая широта лучше описывает астрономическую ситуацию, и поэтому она будет использоваться в формулах расчета. При использовании геоцентрической широты это будет оговариваться дополнительно.

Локальная сфера

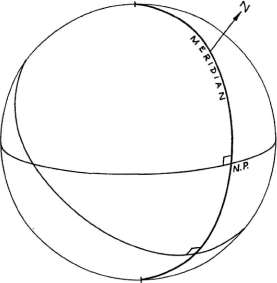Рисунок 1-5

     Часовым кругом называется большой круг, проходящий через северный и южный полюс Мира. Меридиан является часовым кругом, проходящим через зенит и надир (рисунок 1-5). Поскольку он проходит через полюса экватора и горизонта, то он перпендикулярен обоим этим большим кругам. Северная точка (N.P.) горизонта находится на пересечении меридиана и горизонта на северной стороне экватора. Южная точка горизонта находится с противоположной стороны (рисунок 1-5).
    Вертикальный круг является кругом, проходящим через надир и зенит, однако все вертикальные круги пересекают горизонт под прямым углом. Очевидно, что меридиан является одновременно вертикальным и часовым большим кругом.

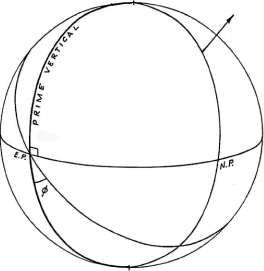Рисунок 1-6

    Первый вертикал (рисунок 1-6) является вертикальным кругом, чьими полюсами являются северная и южная точки горизонта. Первый вертикал пересекает горизонт в той же точке, в которой экватор пересекает горизонт сверху вниз. Эта точка называется точкой Востока (Е.Р.), противоположно ей на горизонте лежит точка Запада, в которой экватор пересекает горизонт снизу вверх. Эти точки Востока и Запада являются полюсами меридиана. Угол между первым вертикалом и экватором равняется географической широте места (ф).
    Координатная система, определяемая горизонтом, меридианом и первым вертикалом называется локальной или мунданной (земной) системой. В этой системе строится сетка домов, в отличие от универсальной системы, в которой строится система знаков.

Универсальная сфера

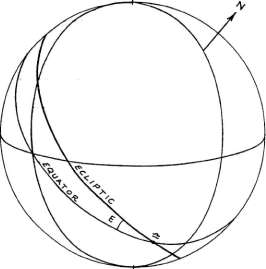Рисунок 1-7

     Эклиптика является большим кругом, показывающим путь Солнца по небесной сфере (рисунок 1-7). Точка в которой эклиптика пересекает экватор называется точкой Овна (Солнце пересекает эту точку с юга на север приблизительно 21 Марта) и противоположная точка Весов (Солнце пересекает эту точку с севера на юг приблизительно 24 Сентября). На рисунке 1-7 показана точка Весов, которая находится восточнее меридиана. Круг широты является большим кругом, который проходит через полюса эклиптики, то есть пересекает эклиптику под прямым углом.
     Угол между небесным экватором и эклиптикой известен как наклон эклиптики (Е). Его величину определяют по следующей формуле:
Е = 23,4523 - 0,013*Т
где Т есть коэффициент столетия от 1 января 1900 года (положительный после этой даты и отрицательный до неё).
    Например:
    дата 14 ноября 1948 представляется в виде 1948,87
    отсюда Т = 0,4887
    Е = 23,4523 - 0,013*0,4887 = 23,4459
     Существует две координатных системы, которые используют локальные точки небесной сферы в применении к универсальной сфере: экваториальная и зодиакальная координатные системы.

Прямое восхождение и склонение

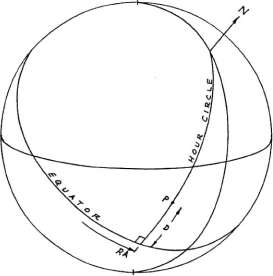Рисунок 1-8

     В экваториальной координатной системе (рисунок 1-8) положение точки Р определяется прямым восхождением (RA) и склонением (D). Прямое восхождение точки Р определяется дугой, проходящей вдоль экватора от точки Овна (к югу от эклиптики), до пересечения с часовым кругом, проходящим через эту точку Р. Дуга, измеряемая вдоль этого часового круга, от экватора до точки Р, называется склонением точки.

Долгота и широта

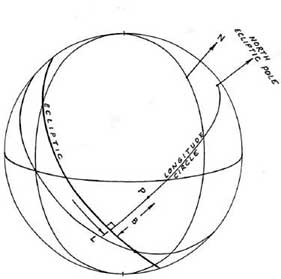Рисунок 1-9

     В зодиакальной координатной системе (рисунок 1-9) положение точки Р определяется долготой (L) и широтой (В). Долгота точки определяется как дуга эклиптики, от точки Овна до пересечения с кругом долготы, проходящем через точку Р. Дуга вдоль круга долготы от эклиптики до точки равняется широте точки Р.
    Склонение и долгота будут иметь положительные значения, если точка лежит севернее экватора или эклиптики, и соответственно отрицательные значения, если точка лежит южнее экватора или эклиптики.
    Большинство эфемерид содержат значения склонения, долготы и широты планеты, но не её прямое восхождение. RA можно расчитать из L, В и D по формуле:
    cos(RA) = cos(L)*cos(В)/ cos(D)

Угловые точки

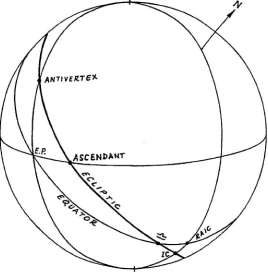Рисунок 1-10

     Точка, в которой эклиптика пересекает горизонт с восточной стороны меридиана (рисунок 1-10) называется Асцендентом (ASC); противоположная точка называется Десцендентом (DSC).
     Точка в которой эклиптика пересекает меридиан с севера от Первого вертикала называется Нижний меридиан (IC); противоположная ей точка называется Серединой неба (MC).
     Точка с которой эклиптика пересекает Первый вертикал с западной стороны меридиана называется Вертекс (VTX); противоположная ей точка называется Антивертекс (AVTX).
    Точка пересечения экватора с меридианом севернее Первого вертикала называется RAIC; противоположная ей точка называется RAMC.
    Прямое восхождение точки Востока определяется как RAMC + 90; и прямое восхождение точки Запада как RAMC - 90. Значение RAMC принято выражать в градусах. Его можно выразить в часах, используя Звездное Время, потому как RAMC численно равен 15*Звездное время.
    Значение МС может быть вычислено при помощи RAMC, используя формулу А3 из Приложения. Значение ASC может быть вычислено из ф и RAMC, используя формулу А8 из Приложения; значение VTX может быть рассчитано по этой же формуле, если взять со-ф вместо ф и RAIC вместо RAMC.

Меридианнное расстояние

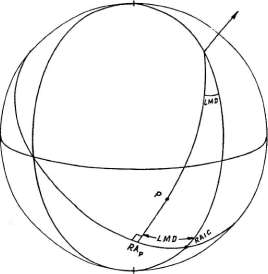Рисунок 1-11

     Верхнее меридианное расстояние (UMD) точки определяется как дуга, направленная вдоль экватора, от RAMC до пересечения с часовым кругом, на котором находится точка. Эта дуга численно равна
|RAMC - RA|, где RA - прямое восхождение точки.
     Нижнее меридианное расстояние (LMD) точки Р (рисунок 1-11) определяется как дуга, направленная вдоль экватора, от RAIC до пересечения с часовым кругом проходящим через точку Р. Эта дуга численно равна |RAIC - RA|
     Очевидно, что раз RAIC = RAMC + 180, то и LMD = 180 - UMD.      Меридианное расстояние (MD) точки равно либо UMD либо LMD, в зависимости от того, какое из этих чисел меньше. Другими словами, MD точки есть угол между часовым кругом, проходящим через эту точку, и ближайшим меридианом (северным или южным).

Полудуги

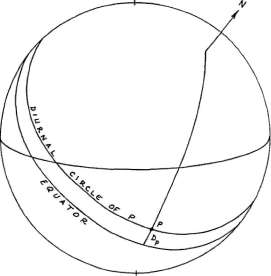Рисунок 1-12

     Дневной круг точки Р (рисунок 1-12) представляет собой малый круг, параллельный экватору и проходящий через эту точку.
    Рисунок 1-13 показывает небесную сферу, спроецированную на Первый вертикал, так что меридиан выглядит вертикальной линией, проходящей через центр.

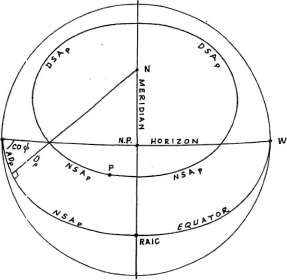Рисунок 1-13

    Часть дневного круга точки, которая лежит ниже горизонта на широте наблюдателя, называется ночной дугой точки; половина этой дуги (промежуток между сторонами нижнего квадранта) называется ночной полудугой (NSA) точки. Аналогично, часть дневного круга точки, который лежит выше горизонта на широте наблюдателя, называется дневной дугой точки; половина этой дуги (промежуток между сторонами верхнего квадранта), называется дневной полудугой (DSA) точки.
    Термин полудуга (SA) будет использоваться для обозначения DSA, если точка находится выше линии горизонта и NSA если точка находится ниже линии горизонта.

Разница восхождений

     Рассмотрим треугольник, сторонами которого являются дуги горизонта, экватора и часового круга, который пересекает горизонт и дневной круг точки Р (рисунок 1-13). Дуга вдоль часового круга численно равна D, или склонению точки. Противоположный угол (между горизонтом и экватором) равняется co-ф, то есть дополняет широту наблюдателя до 90 градусов. Дуга вдоль экватора от точки Востока до пересечения с часовым кругом называется разницей восхождений (AD) точки.
    Из формулы сферической геометрии получаем что: sin(AD) = tg(D)*ctg(со-ф) .
    Отсюда следует формула 1-1:
    AD = Arcsin(tg(D)*tg(ф)), где D - склонение, а ф - широта наблюдателя.
    Так как D и ф имеют положительные значение в северных широтах и отрицательные в южных, AD будет иметь отрицательное значение когда D и ф находятся в противоположных сферах.
    Так как дуга вдоль экватора от точки Востока до RAIC равна 90, то значение NSA для точки будет равно 90 - AD. Ночные и дневные полудуги точки определяются по формуле 1-2:
    NSA = 90 - AD;
    DSA = 90 + AD.
    Пример:
    ф = 51 N 30
    если D(su) = 18 S 23 тогда NSA(su) = 114,70
    если D(mo) = 11 N 14 тогда DSA(mo) = 104,46

Квадранты

    Круги меридиана и горизонта разрезают небесную сферу на четыре области, которые называются квадрантами.
    Первый квадрант (дома 1,2 и 3 в большинстве систем домов) вырезает дугу на Первом вертикале от точки Востока до надира.
    Второй квадрант (дома 4,5 и 6) вырезает дугу на Первом вертикале от надира до точки Запада.
    Третий квадрант (дома 7,8 и 9) вырезает дугу на Первом вертикале от точки Запада до зенита.
    Четвертый квадрант (дома 10,11 и 12) вырезает дугу на Первом вертикале от зенита до точки Востока.
    Не всегда возможно точно определить, в каком квадранте локализовано тело при анализе гороскопа. Например, точка на эклиптике, отражающая долготу тела, может пересечь меридиан после того, как это сделает само тело (как это было в случае с кометой в гороскопе Принца Charles), и в таком случае гороскоп будет показывать тело не c той стороны меридиана.
    Для того, чтобы однозначно определять квадрант, в котором находится тело, необходимо решить, оно находится восточнее (RAMC < RA < RAIC) или западнее (RAIC < RA < RAMC) меридиана, а также выше (UMD < DSA или LMD > NSA) или ниже (UMD > DSA или LMD < NSA) горизонта.
    Если тело находится в первом квадранте, то оно лежит восточнее меридиана и ниже горизонта.
    Если тело находится во втором квадранте, то оно лежит западнее меридиана и ниже горизонта.
    Если тело находится в третьем квадранте, то оно лежит западнее меридиана и выше горизонта.
    Если тело находится в четвертом квадранте, то оно лежит восточнее меридиана и выше горизонта.
    Такое определение квадрантов соответствует таким системам домов, как Кампануса, Региомонтана и Плацидуса. Однако в системе домов Порфирия квадранты определяются по-другому, о чем будет сказано в главе, посвященной этой системе.

Мунданная позиция

    Мунданная позиция (МР) тела определяется как его локальная позиция по отношению к домам гороскопа, то есть это позиция тела в локальной сфере в выбранной системе домов. Термин "Мунданная позиция" используется в данной книге в трех близких значениях:
    Во первых, Мунданная позиция тела обозначает положение множества точек на небесной сфере, которые находятся в соединении с телом (согласно правилам построения выбранной системы домов). Если местоположением этих точек является большой круг небесной сферы, то тогда этот круг определяется как проекционный круг и выбранная система домов называется проекционной системой.
    Во вторых, иногда удобно для целей вычисления принять одну из точек, находящихся в соединении с телом, как представителя всего множества и расчеты МР производить только с ней.
    В третьих, Мунданную позицию тела можно определить числом в интервале от 0 до 360, которое определяет положение тела на локальной сфере. Эта числовая Мунданная позиция соответствует двум условиям:
    Условие А: Числовое Мунданное положение N-ного куспида дома (то есть МР точки эклиптики с долготой N-ного куспида дома) определяется как: MP = 360*(N - 1)/M , где М есть полное число домов. Обычно М = 12, но астрологи используют как 8 так и 24 дома.
    В случае 12 домов, куспиду первого дома присваивается Мунданная позиция 0; куспиду второго дома присваивается МР = 30; куспиду третьего дома МР = 60; и так далее. Выбор начала куспида первого дома является произвольным и лежит в интервале от 0 до 360. Например, в Горизонтальной системе домов числовая Мунданная позиция (азимут) равна нулю на куспиде четвертого дома, вместо первого. А в системе домов Региомонтана числовая Мунданная позиция (наклонное восхождение под собственным полюсом) равна нулю в точке Овна, и не зависит от того, какой дом на неё попадает.
    Условие B: Две точки находятся в соединении согласно правилам данной системы домов, если они имеют одинаковую числовую Мунданную позицию.

Copyright© 2004 STELLIUM.RU  Webmaster